lesson 8 homework 5.5 answer key

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Eureka Math Grade 8 Module 5 Lesson 8 Answer Key

Engage ny eureka math 8th grade module 5 lesson 8 answer key, eureka math grade 8 module 5 lesson 8 exploratory challenge/exercise answer key.

Exercise 1. Consider the function that assigns to each number x the value x 2 . a. Do you think the function is linear or nonlinear? Explain. Answer: I think the function is nonlinear. The equation describing the function is not of the form y = mx + b.

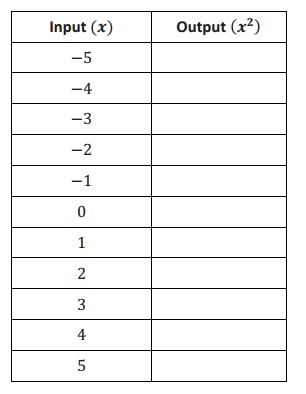
d. What shape does the graph of the points appear to take? Answer: It appears to take the shape of a curve.

e. Find the rate of change using rows 1 and 2 from the table above. Answer: \(\frac{25 – 16}{ – 5 – ( – 4)}\) = \(\frac{9}{ – 1}\) = – 9

f. Find the rate of change using rows 2 and 3 from the table above. Answer: \(\frac{16 – 9}{ – 4 – ( – 3)} = \) = \(\frac{7}{ – 1}\) = – 7

g. Find the rate of change using any two other rows from the table above. Answer: Student work will vary. \(\frac{16 – 25}{4 – 5}\) = \(\frac{ – 9}{ – 1}\) = 9

h. Return to your initial claim about the function. Is it linear or nonlinear? Justify your answer with as many pieces of evidence as possible. Answer: This is definitely a nonlinear function because the rate of change is not a constant for different intervals of inputs. Also, we would expect the graph of a linear function to be a set of points in a line, and this graph is not a line. As was stated before, the expression x 2 is nonlinear.

Exercise 2. Consider the function that assigns to each number x the value x 3 . a. Do you think the function is linear or nonlinear? Explain. Answer: I think the function is nonlinear. The equation describing the function is not of the form y = mx + b.

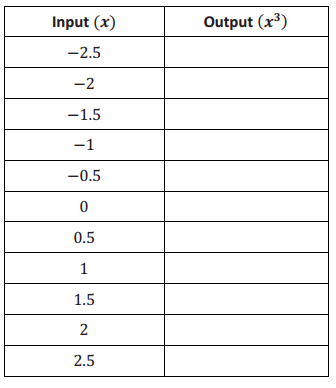
e. Find the rate of change using rows 2 and 3 from the table above. Answer: \(\frac{ – 8 – ( – 3.375)}{ – 2 – ( – 1.5)}\) = \(\frac{ – 4.625}{ – 0.5}\) = 9.25

f. Find the rate of change using rows 3 and 4 from the table above. Answer: \(\frac{ – 3.375 – ( – 1)}{ – 1.5 – ( – 1)}\) = \(\frac{ – 2.375}{ – 0.5}\) = 4.75

g. Find the rate of change using rows 8 and 9 from the table above. Answer: \(\frac{1 – 3.375}{1 – 1.5}\) = \(\frac{ – 2.375}{ – 0.5}\) = 4.75

h. Return to your initial claim about the function. Is it linear or nonlinear? Justify your answer with as many pieces of evidence as possible. Answer: This is definitely a nonlinear function because the rate of change is not a constant for any interval of inputs. Also, we would expect the graph of a linear function to be a line, and this graph is not a line. As was stated before, the expression x 3 is nonlinear.

Exercise 3. Consider the function that assigns to each positive number x the value \(\frac{1}{x}\). a. Do you think the function is linear or nonlinear? Explain. Answer: I think the function is nonlinear. The equation describing the function is not of the form y = mx + b.

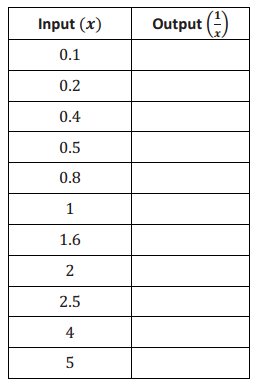
e. Find the rate of change using rows 1 and 2 from the table above. Answer: \(\frac{10 – 5}{0.1 – 0.2}\) = \(\frac{5}{ – 0.1}\) = – 50

f. Find the rate of change using rows 2 and 3 from the table above. Answer: \(\frac{5 – 2.5}{0.2 – 0.4}\) = \(\frac{2.5}{ – 0.2}\) = – 12.5

g. Find the rate of change using any two other rows from the table above. Answer: Student work will vary. \(\frac{1 – 0.625}{1 – 1.6}\) = \(\frac{0.375}{ – 0.6}\) = – 0.625

h. Return to your initial claim about the function. Is it linear or nonlinear? Justify your answer with as many pieces of evidence as possible. Answer: This is definitely a nonlinear function because the rate of change is not a constant for any interval of inputs. Also, we would expect the graph of a linear function to be a line, and this graph is not a line. As was stated before, the expression \(\frac{1}{x}\) is nonlinear.

Exercises 4–10 In each of Exercises 4–10, an equation describing a rule for a function is given, and a question is asked about it. If necessary, use a table to organize pairs of inputs and outputs, and then plot each on a coordinate plane to help answer the question.

Eureka Math Grade 8 Module 5 Lesson 8 Problem Set Answer Key

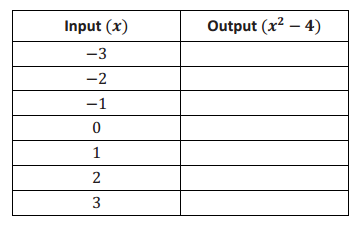
Question 1. Consider the function that assigns to each number x the value x 2 – 4. a. Do you think the function is linear or nonlinear? Explain. Answer: The equation describing the function is not of the form y = mx + b. It is not linear.

b. Do you expect the graph of this function to be a straight line? Answer: No

Question 2. Consider the function that assigns to each number x greater than – 3 the value \(\frac{1}{x + 3}\). a. Is the function linear or nonlinear? Explain. Answer: The equation describing the function is not of the form y = mx + b. It is not linear.

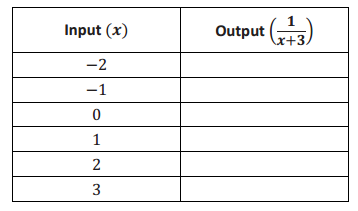
d. Was your prediction to (b) correct? Answer: Yes, the graph appears to be taking the shape of some type of curve.

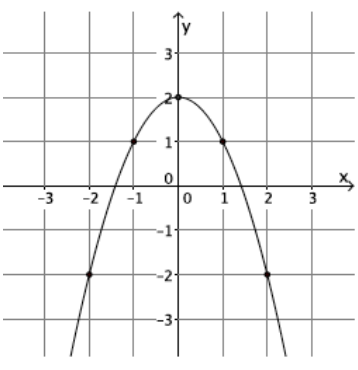
b. What is the average rate of change for this function from an input of x = – 2 to an input of x = – 1? Answer: \(\frac{ – 2 – 1}{ – 2 – ( – 1)}\) = \(\frac{ – 3}{ – 1}\) = 3

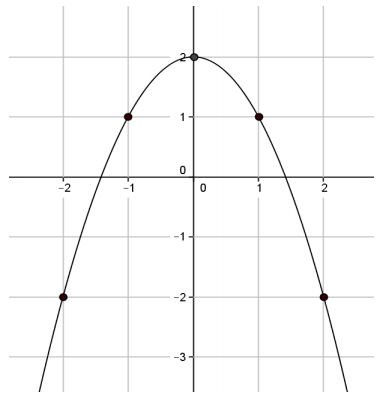
Eureka Math Grade 8 Module 5 Lesson 8 Exit Ticket Answer Key

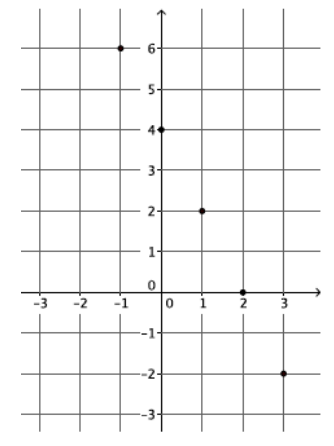
Question 2. Consider the function that assigns to each number x the value \(\frac{1}{2}\) x 2 . Do you expect the graph of this function to be a straight line? Briefly justify your answer. Answer: The equation is nonlinear (not of the form y = mx + b), so the function is nonlinear. Its graph will not be a straight line.

Submit Your Question

• Texas Go Math
• Big Ideas Math
• enVision Math
• EngageNY Math
• McGraw Hill My Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Texas Go Math Grade 5 Lesson 5.5 Answer Key Add and Subtract Fractions

Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 5.5 Answer Key Add and Subtract Fractions.

Unlock the Problem

Malia bought shell beads and glass beads to weave into designs in her baskets. She bought \(\frac{1}{4}\) pound of shell beads and \(\frac{3}{8}\) pound of glass beads. How many pounds of beads did she buy?

• Underline the question you need to answer.
• Draw a circle around the information you will use.

Add. \(\frac{1}{4}\) + \(\frac{3}{8}\). Write your answer in simplest form.

Another Way

So, Malia bought _________ pound of beads. Answer:

Another Way The least common denominator of 1 4  and  3 8 is 8

So, Malia bought \(\frac{5}{8}\)  pound of beads.

Lesson 5.5 Go Math Grade 5 Answer Key Question 1. Explain how you know whether your answer is reasonable. Answer: Both methods are the same they both give the same answer The least common denominator is the simplest method

When subtracting two fractions with unequal denominators, follow the same steps you follow when adding two fractions. However, instead of adding the fractions, subtract.

Question 2. Explain how you know whether your answer is reasonable. Answer: The fraction solved into simplest form is reasonable which found by least common denominator

Share and Show

Find the sum or difference. Write your answer in simplest form.

Question 1. \(\frac{5}{12}\) + \(\frac{1}{3}\) Answer: \(\frac{5}{12}\) + \(\frac{1}{3}\) = \(\frac{5}{12}\) + \(\frac{4}{12}\) = \(\frac{9}{12}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 2. \(\frac{2}{5}\) + \(\frac{3}{7}\) Answer: \(\frac{2}{5}\) + \(\frac{3}{7}\) = \(\frac{14}{35}\) + \(\frac{15}{35}\) =\(\frac{29}{35}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 3. \(\frac{1}{6}\) + \(\frac{3}{4}\) Answer: \(\frac{1}{6}\) + \(\frac{3}{4}\) = \(\frac{2}{12}\) + \(\frac{9}{12}\) = \(\frac{11}{12}\) Explanation: Step 1: The least common denominator is found Step 2: write equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Lesson 5.5 Answer Key Go Math Grade 5 Question 4. \(\frac{3}{4}\) – \(\frac{1}{8}\) Answer: \(\frac{3}{4}\) – \(\frac{1}{8}\) = \(\frac{6}{8}\) – \(\frac{1}{8}\) = \(\frac{5}{8}\) Explanation: Step 1: The least common denominator is found Step 2: write equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 5. \(\frac{1}{4}\) – \(\frac{1}{7}\) Answer: \(\frac{1}{4}\) – \(\frac{1}{7}\) = \(\frac{7}{28}\) – \(\frac{4}{28}\)= \(\frac{3}{28}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 6. \(\frac{9}{10}\) – \(\frac{1}{4}\) Answer: \(\frac{9}{10}\) – \(\frac{1}{4}\) = \(\frac{18}{20}\) – \(\frac{5}{20}\)= \(\frac{13}{20}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Math Talk Mathematical Processes

Explain why it is important to check your answer for reasonableness. Answer:

Problem Solving

Practice: Copy and Solve Find the sum or difference. Write your answer in simplest form.

Question 7. \(\frac{1}{3}\) + \(\frac{4}{18}\) Answer: \(\frac{1}{3}\) + \(\frac{4}{18}\) = \(\frac{6}{18}\) + \(\frac{4}{18}\) =\(\frac{10}{18}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 8. \(\frac{3}{5}\) + \(\frac{1}{3}\) Answer: \(\frac{3}{5}\) + \(\frac{1}{3}\) = \(\frac{9}{15}\) + \(\frac{5}{15}\) = \(\frac{14}{15}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 9. \(\frac{3}{10}\) + \(\frac{1}{6}\) Answer: \(\frac{3}{10}\) + \(\frac{1}{6}\) = \(\frac{9}{30}\) + \(\frac{5}{30}\) = \(\frac{14}{30}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 10. \(\frac{1}{2}\) + \(\frac{4}{9}\) Answer: \(\frac{1}{2}\) + \(\frac{4}{9}\) = \(\frac{9}{18}\) + \(\frac{8}{18}\) = \(\frac{17}{18}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Go Math Grade 5 Lesson 5.5 Answer Key Question 11. \(\frac{1}{2}\) – \(\frac{3}{8}\) Answer: \(\frac{1}{2}\) – \(\frac{3}{8}\) = \(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 12. \(\frac{5}{7}\) – \(\frac{2}{3}\) Answer: \(\frac{5}{7}\) – \(\frac{2}{3}\) = \(\frac{15}{21}\) – \(\frac{14}{21}\) = \(\frac{1}{21}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 13. \(\frac{4}{9}\) – \(\frac{1}{6}\) Answer: \(\frac{4}{9}\) – \(\frac{1}{6}\) = \(\frac{8}{18}\) – \(\frac{3}{18}\) = \(\frac{5}{18}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 14. \(\frac{11}{12}\) – \(\frac{7}{15}\) Answer: \(\frac{11}{12}\) – \(\frac{7}{15}\) = \(\frac{55}{60}\) – \(\frac{28}{60}\) = \(\frac{27}{60}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

H.O.T. Algebra Find the unknown number.

Question 15. \(\frac{9}{10}\) – ☐ = \(\frac{1}{5\) ☐ = ___________ Answer: \(\frac{9}{10}\) – \(\frac{7}{10}\)= \(\frac{1}{5\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 16. \(\frac{5}{12}\) + ☐ = \(\frac{1}{2}\) ☐ = ____________ Answer: \(\frac{5}{12}\) + \(\frac{1}{12}\) =\(\frac{6}{12}\) =\(\frac{1}{2}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Go Math Grade 5 Lesson 5.5 Practice Answer Key Question 17. Sara is making a key chain using the bead design shown. What fraction of the beads in her design are either blue or red? Answer: Explanation: Let us consider dark black as red and light black-as-blue The number of beads is 15 Number of red beads are \(\frac{5}{15}\) Number of black beads are \(\frac{6}{15}\)

Question 19. Write Math Jamie had \(\frac{4}{5}\) of a spool of twine. He then used \(\frac{1}{2}\) of a spool of twine to make friendship knots. He claims to have \(\frac{3}{10}\) of the original spool of twine leftover. How you know whether Jamie’s claim is reasonable. Answer: Yes. Jamie’s claim is reasonable. Explanation: Jamie had \(\frac{4}{5}\) of a spool of twine. He then used \(\frac{1}{2}\) of a spool of twine to make friendship knots.  So \(\frac{3}{10}\) of the original spool of twine leftover. Since \(\frac{4}{5}\) –\(\frac{1}{2}\) = \(\frac{8}{10}\) – \(\frac{5}{10}\) = \(\frac{3}{10}\) He claims to have \(\frac{3}{10}\) of the original spool of twine leftover. So it is equla to what he leftover. So his claim is reasonabale.

Daily Assessment Task

Fill in the bubble completely to show your answer.

Question 20. Apply Students are voting for a new school mascot. So far, the results show that \(\frac{3}{10}\) of the students voted for “Fightin’ Titan,” \(\frac{1}{2}\) of the students voted for “Nifty Knight,” and the rest of the students have not voted yet. What fraction of the student population has not voted yet? (A) \(\frac{3}{10}\) (B) \(\frac{2}{5}\) (C) \(\frac{1}{5}\) (D) \(\frac{4}{5}\) Answer: (C) \(\frac{1}{5}\) Explanation: So far, the results show that \(\frac{3}{10}\) of the students voted for “Fightin’ Titan,” \(\frac{1}{2}\) of the students voted for “Nifty Knight,” Then \(\frac{8}{10}\) voted. Since \(\frac{3}{10}\) +\(\frac{1}{2}\) = \(\frac{8}{10}\) So \(\frac{1}{5}\) of the students have not voted yet. Since 1- \(\frac{8}{10}\) = \(\frac{1}{5}\)

Question 21. Tina spent \(\frac{3}{5}\) of her paycheck on a trip to the beach. She spent \(\frac{3}{8}\) of her paycheck on new clothes for the trip. What fraction of her paycheck did Tina spend on the trip and clothes together? (A) \(\frac{9}{40}\) (B) \(\frac{3}{4}\) (C) \(\frac{7}{8}\) (D) \(\frac{39}{40}\) Answer: (D) \(\frac{39}{40}\) Explanation: Tina spent \(\frac{3}{5}\) of her paycheck on a trip to the beach. She spent \(\frac{3}{8}\) of her paycheck on new clothes for the trip. So Tortal Spent is \(\frac{39}{40}\) \(\frac{3}{5}\) + \(\frac{3}{8}\)  = \(\frac{39}{40}\)

Question 22. Multi-Step On Friday, \(\frac{1}{6}\) of band practice was spent trying on uniforms. The band spent \(\frac{1}{4}\) of practice on marching. What fraction of practice time was left for playing music? (A) \(\frac{5}{12}\) (B) \(\frac{1}{2}\) (C) \(\frac{7}{12}\) (D) \(\frac{1}{4}\) Answer: (C) \(\frac{7}{12}\) Explanation: \(\frac{1}{6}\) of band practice was spent trying on uniforms. The band spent \(\frac{1}{4}\) of practice on marching. So Total time spent is \(\frac{5}{12}\). So Time left is \(\frac{7}{12}\) \(\frac{1}{6}\) + \(\frac{1}{4}\) = \(\frac{5}{12}\) 1-\(\frac{5}{12}\) =\(\frac{7}{12}\)

Texas Test Prep

Texas Go Math Grade 5 Lesson 5.5 Homework and Practice Answer Key

Question 1. \(\frac{1}{5}\) + \(\frac{1}{2}\) ____________ Answer: \(\frac{1}{5}\) + \(\frac{1}{2}\) = \(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\) Explanation: Step 1: The least common denominator is found Step 2: write equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Go Math Grade 5 Lesson 5.5 Answer Key Question 2. \(\frac{2}{3}\) + \(\frac{1}{6}\) ____________ Answer: \(\frac{2}{3}\) + \(\frac{1}{6}\) = \(\frac{4}{6}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 3. \(\frac{1}{4}\) + \(\frac{2}{3}\) ____________ Answer: \(\frac{1}{4}\) + \(\frac{2}{3}\) = \(\frac{3}{12}\) + \(\frac{8}{12}\) = \(\frac{11}{12}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 4. \(\frac{3}{4}\) + \(\frac{1}{8}\) ____________ Answer: \(\frac{3}{4}\) + \(\frac{1}{8}\) = \(\frac{6}{8}\) + \(\frac{1}{8}\) = \(\frac{7}{8}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 5. \(\frac{2}{9}\) + \(\frac{1}{3}\) ____________ Answer: \(\frac{2}{9}\) + \(\frac{1}{3}\) = \(\frac{2}{9}\) + \(\frac{3}{9}\) = \(\frac{5}{9}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 6. \(\frac{1}{2}\) + \(\frac{2}{6}\) ____________ Answer: \(\frac{1}{2}\) + \(\frac{2}{6}\) = \(\frac{3}{6}\) + \(\frac{2}{6}\) = \(\frac{5}{6}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 7. \(\frac{3}{10}\) + \(\frac{1}{3}\) ____________ Answer: \(\frac{3}{10}\) + \(\frac{1}{3}\) = \(\frac{9}{30}\) + \(\frac{10}{30}\) = \(\frac{19}{30}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 8. \(\frac{4}{18}\) + \(\frac{2}{6}\) ____________ Answer: \(\frac{4}{18}\) + \(\frac{2}{6}\) = \(\frac{4}{18}\) + \(\frac{6}{18}\) = \(\frac{10}{18}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 9. \(\frac{6}{12}\) – \(\frac{1}{3}\) ____________ Answer: \(\frac{6}{12}\) – \(\frac{1}{3}\) = \(\frac{6}{12}\) – \(\frac{4}{12}\) = \(\frac{2}{12}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 10. \(\frac{3}{4}\) – \(\frac{1}{6}\) ____________ Answer: \(\frac{3}{4}\) – \(\frac{1}{6}\) = \(\frac{9}{12}\) – \(\frac{2}{12}\) = \(\frac{7}{12}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 11. \(\frac{5}{7}\) – \(\frac{1}{2}\) ____________ Answer: \(\frac{5}{7}\) – \(\frac{1}{2}\) = \(\frac{10}{14}\) – \(\frac{7}{14}\) = \(\frac{3}{14}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 12. \(\frac{8}{9}\) – \(\frac{2}{3}\) ____________ Answer: \(\frac{8}{9}\) – \(\frac{2}{3}\) = \(\frac{8}{9}\) – \(\frac{6}{9}\) = \(\frac{2}{9}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 13. \(\frac{5}{9}\) – \(\frac{1}{6}\) ____________ Answer: \(\frac{5}{9}\) – \(\frac{1}{6}\) = \(\frac{10}{18}\) – \(\frac{3}{18}\) = \(\frac{7}{18}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 14. \(\frac{2}{3}\) – \(\frac{1}{4}\) ____________ Answer: \(\frac{2}{3}\) – \(\frac{1}{4}\) = \(\frac{8}{12}\) – \(\frac{3}{12}\) = \(\frac{5}{12}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 15. \(\frac{7}{14}\) – \(\frac{2}{7}\) ____________ Answer: \(\frac{7}{14}\) – \(\frac{2}{7}\) = \(\frac{7}{14}\) – \(\frac{4}{14}\) = \(\frac{3}{14}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 16. \(\frac{5}{6}\) – \(\frac{3}{4}\) ____________ Answer: \(\frac{5}{6}\) – \(\frac{3}{4}\) = \(\frac{10}{12}\) – \(\frac{9}{12}\) = \(\frac{1}{12}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Find the unknown number.

Question 17. \(\frac{7}{12}\) – ☐ = \(\frac{1}{6}\) ☐ = _____________ Answer: \(\frac{7}{12}\) – \(\frac{5}{12}\) = \(\frac{1}{6}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 18. \(\frac{5}{18}\) + ☐ = \(\frac{1}{2}\) ☐ = _____________ Answer: \(\frac{5}{18}\) + \(\frac{4}{18}\) = \(\frac{1}{2}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 19. \(\frac{7}{10}\) – ☐ = \(\frac{2}{5}\) ☐ = ______________ Answer: \(\frac{7}{10}\) – \(\frac{3}{10}\) = \(\frac{2}{5}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 20. ☐ + \(\frac{1}{9}\) = \(\frac{1}{3}\) ☐ = _______________ Answer: \(\frac{2}{9}\) + \(\frac{1}{9}\) = \(\frac{1}{3}\) Explanation: Step 1: The least common denominator is found Step 2: written equivalent fractions with equal denominators Step 3: write the answer in simplest form.

Question 21. There are 12 students in the pep squad. Three students are wearing white shirts. Six students are wearing blue shirts. What fraction of the students in the pep squad are wearing either white or blue shirts? Answer: \(\frac{1}{4}\)  wearing the white shirts and \(\frac{1}{2}\) wearing the blue shirts. Explanation: There are 12 students in the pep squad. Three students are wearing white shirts. \(\frac{3}{12}\)  = \(\frac{1}{4}\) Six students are wearing blue shirts. \(\frac{6}{12}\)  = \(\frac{1}{2}\)

Question 22. Tiffany ran \(\frac{5}{6}\) mile. Shayne ran \(\frac{3}{4}\) mile. Who ran farther? How much farther? Answer:

Lesson Check

Question 23. Mr. Benson spent \(\frac{2}{5}\) of the monthly budget on rent and \(\frac{3}{10}\) of the budget on food. What fraction of Mr. Benson’s budget was spent on rent and food? (A) \(\frac{1}{3}\) (B) \(\frac{3}{10}\) (C) \(\frac{7}{10}\) (D) \(\frac{1}{2}\) Answer: (C) \(\frac{7}{10}\) Explanation: Mr. Benson spent \(\frac{2}{5}\) of the monthly budget on rent and \(\frac{3}{10}\) of the budget on food. Sum of \(\frac{2}{5}\) and \(\frac{3}{10}\)  is \(\frac{7}{10}\) . Since \(\frac{3}{10}\)+ \(\frac{2}{5}\)= \(\frac{7}{10}\) .

Question 24. The Ortega family made \(\frac{15}{16}\) pound of confetti for the annual Fiesta celebration in San Antonio. They used \(\frac{1}{4}\) pound to make confetti filled eggs. How much confetti is left to use next year? (A) \(\frac{11}{16}\) pound (B) \(\frac{9}{16}\) pound (C) \(\frac{4}{5}\) pound (D) \(\frac{3}{4}\) pound Answer: (A) \(\frac{11}{16}\) pound Explanation: The Ortega family made \(\frac{15}{16}\) pound of confetti for the annual Fiesta celebration in San Antonio. They used \(\frac{1}{4}\) pound to make confetti filled eggs. confetti is left to use next year is \(\frac{11}{16}\) pound. Since

\(\frac{15}{16}\) – \(\frac{1}{4}\) = \(\frac{11}{16}\) pound

Question 25. If Rory measures the lemon juice and the vanilla extract into one spoon before adding them to the blender, how much liquid will be in the spoon? (A) \(\frac{5}{8}\) teaspoon (B) \(\frac{1}{5}\) teaspoon (C) \(\frac{1}{4}\) teaspoon (D) \(\frac{3}{8}\) teaspoon Answer: (A) \(\frac{5}{8}\) teaspoon Explanation: Sum of lemon juice and the vanilla extract is \(\frac{1}{2}\) teaspoon + \(\frac{1}{8}\) teaspoon = \(\frac{5}{8}\) teaspoon

Question 26. Multi-Step Rory has \(\frac{5}{8}\) cup of milk. How much milk does she have left after she doubles the recipe for the smoothie? (A) \(\frac{3}{8}\) cup (B) \(\frac{1}{8}\) cup (C) \(\frac{3}{4}\) cup (D) \(\frac{1}{2}\) cup Answer: (B) \(\frac{1}{8}\) cup Explanation: she doubles the recipe for the smoothie. So it is \(\frac{1}{2}\) cup. Since \(\frac{1}{4}\) cup + \(\frac{1}{4}\) cup  = \(\frac{1}{2}\) cup. Rory has \(\frac{5}{8}\) cup of milk. She left \(\frac{1}{8}\) cup of milk. Since \(\frac{5}{8}\)  –\(\frac{1}{2}\) cup. = \(\frac{1}{8}\)

Question 27. Multi-Step Torn has \(\frac{7}{8}\) cup of olive oil. He uses \(\frac{1}{2}\) cup to make salad dressing and \(\frac{1}{4}\) cup to make tomato sauce. How much olive oil does Torn have left? (A) \(\frac{5}{4}\) cups (B) \(\frac{5}{8}\) cup (C) \(\frac{3}{8}\) cup (D) \(\frac{1}{8}\) cup Answer: (D) \(\frac{1}{8}\) cup Explanation: \(\frac{1}{2}\) + \(\frac{1}{4}\)  = \(\frac{3}{4}\) and \(\frac{7}{8}\) cup – \(\frac{3}{4}\) cup = \(\frac{1}{8}\) cup

Share this:

Leave a comment cancel reply.

You must be logged in to post a comment.