research methodology descriptive statistics

Descriptive Research

Descriptive statistics and their important role in research.

Data and statistics are often used in research but these two terms have different distinctions. Data refers to the pieces of information recorded and gathered for the purpose of analysis. Descriptive statistics, on the other hand, is the result of the analysis made through the data gathered.

In order for you to be able to gather data in your statistical study, you have to first determine the population – which can be a group of people, or things, depending on the subject of your descriptive research . A collection of data of one or more variables is called a data set. A variable has two main types: categorical and numerical. Categorical represents data that is qualitative while numerical represents quantitative data. A categorical variable can either be nominal or ordinal. On the other hand, numerical variables are either discrete or continuous. 

Role of Statistics in Research

The role of statistics in research is to be used as a tool in analyzing and summarizing a large volume of raw data and coming up with conclusions on tests being made. The study of statistics is classified into two main branches: descriptive statistics and inferential statistics. Inferential statistics are used for hypotheses testing and estimating the parameters of a population while descriptive statistics is the way of summarizing and organizing sets of data to make it more easily understood by the audience it is meant for. It often describes information through patterns and graphs.

The first and foremost steps being used in data analysis, as it is difficult to analyze raw data in large volumes. Before you are able to go further on your research, you have to first gather and simplify your data sets. 

There are two methods in descriptive statistics: the numerical method and the graphical method. 

Descriptive Statistics and Numerical Methods

Descriptive statistics involves averages, frequencies, and percentages for categorical data, and standard deviations for continuous data. The statistical measures used in descriptive statistics are the measures of central tendency, measures of spread, and measures of skewness.

A measure of central tendency represents the central point of a dataset which involves the mean, median, and mode. Mean, also called as the average, is simply the sum of the data sets divided by the number of terms. The median, on the other hand, is the value in the middle of a data set while the mode is the number that appears the most in a data set.

If the total number of terms in a data set is an even number, you have to get the two values in the middle and solve for its average to be able to get the median. It is also possible to find more than one mode in a data set which is called multimodal. 

A measure of spread, also called as the measure of dispersion, describes the variability of the values in a data set. It involves the computation of range, variance, standard deviation, and quartiles. 

The range tells the value of the distance between the lowest and the hight value. Standard deviation is the measure of dispersion in the center of the value, while the variance is the expectation square of the standard deviation. 

A quartile is classified into three parts: The first quartile or the Q1 is the middle number between the lowest value and the median of the data set. The second quartile (Q2), is the median of the data, while the third quartile (Q3) is the middle value between the median and the highest number in the data set. 

Skewness is the degree of distribution of a variable about its mean. The value of skewness can either be positive, negative, or undefined. When the result is zero, it means that no skewness has occurred.

Descriptive Statistics and Graphical Methods

In descriptive statistics, graphs are used to visualize data analysis and plot data sets. The most common graphs used are pie graphs, bar graphs, line charts, and histograms. Other types of graphs that are less common are the dot plots, and dots and whiskers charts. 

The pie chart is a circular chart to describe a numerical proportion. It is often divided into slices proportionally based on the quantity it represents. In the example below, assume that you created a survey for teenagers to know their top hobbies. On a scale of 100 teens, 40 of them often browse social media which makes it the highest among other hobbies mentioned. Indoor games being 5% based on the pie chart is the least favorite hobby of teenagers. 

Line Charts

A line chart or line graph is a type of chart that illustrates data sets without a specific numerical proportion. It is best and most often used to represent sequential orders and trends over time. For example, you have recently set up a business selling sweet treats. Each week you have used different types of marketing approaches. For you to be able to determine what kind of marketing strategy worked best, you have to illustrate and analyze the sales you’ve made each week. 

Bar graphs illustrate categorical data with vertical or horizontal rectangular bars as their values.  Through a bar graph, the viewer can compare data easily at a glance. Pie charts represent proportion as a whole while bar graphs illustrate each bar with different values or categories. For example, you are selling different ice cream flavors. To know which are the best sellers, you can simply draw a graph presenting each flavor and the number of ice cream being sold. We can easily determine in this graph that the dark chocolate flavor has the most number of ice cream being sold and vanilla being the least among other flavors. 

Analyzing data can be both easy and complicated. With descriptive statistics, we can easily describe and simplify a large volume of raw data and convert it into something that can be easily understood by our viewers. From illustrating the number of sales in the business up to the analysis needed for machine learning, descriptive statistics help us go further beyond every research and know the other steps necessary for data analysis.

Image by  rawpixel

Thanks for Reading

Enjoyed this post? Share it with your networks.

DescriptiveResearch Contributor

Descriptive analysis and its importance in our daily lives.

How does descriptive analysis fit in our daily life? We often hear the word “statistics” in our math classes. However, most of us aren’t aware of the importance of statistics in our life. It plays…

Popular searches

• How to Get Participants For Your Study
• How to Do Segmentation?
• Conjoint Preference Share Simulator
• MaxDiff Analysis
• Likert Scales
• Reliability & Validity

Request consultation

Do you need support in running a pricing or product study? We can help you with agile consumer research and conjoint analysis.

Looking for an online survey platform?

Conjointly offers a great survey tool with multiple question types, randomisation blocks, and multilingual support. The Basic tier is always free.

Research Methods Knowledge Base

• Navigating the Knowledge Base
• Foundations
• Measurement
• Research Design
• Conclusion Validity
• Data Preparation
• Correlation
• Inferential Statistics
• Table of Contents

Descriptive Statistics

Descriptive statistics are used to describe the basic features of the data in a study. They provide simple summaries about the sample and the measures. Together with simple graphics analysis, they form the basis of virtually every quantitative analysis of data.

Descriptive statistics are typically distinguished from inferential statistics . With descriptive statistics you are simply describing what is or what the data shows. With inferential statistics, you are trying to reach conclusions that extend beyond the immediate data alone. For instance, we use inferential statistics to try to infer from the sample data what the population might think. Or, we use inferential statistics to make judgments of the probability that an observed difference between groups is a dependable one or one that might have happened by chance in this study. Thus, we use inferential statistics to make inferences from our data to more general conditions; we use descriptive statistics simply to describe what’s going on in our data.

Descriptive Statistics are used to present quantitative descriptions in a manageable form. In a research study we may have lots of measures. Or we may measure a large number of people on any measure. Descriptive statistics help us to simplify large amounts of data in a sensible way. Each descriptive statistic reduces lots of data into a simpler summary. For instance, consider a simple number used to summarize how well a batter is performing in baseball, the batting average. This single number is simply the number of hits divided by the number of times at bat (reported to three significant digits). A batter who is hitting .333 is getting a hit one time in every three at bats. One batting .250 is hitting one time in four. The single number describes a large number of discrete events. Or, consider the scourge of many students, the Grade Point Average (GPA). This single number describes the general performance of a student across a potentially wide range of course experiences.

Every time you try to describe a large set of observations with a single indicator you run the risk of distorting the original data or losing important detail. The batting average doesn’t tell you whether the batter is hitting home runs or singles. It doesn’t tell whether she’s been in a slump or on a streak. The GPA doesn’t tell you whether the student was in difficult courses or easy ones, or whether they were courses in their major field or in other disciplines. Even given these limitations, descriptive statistics provide a powerful summary that may enable comparisons across people or other units.

Univariate Analysis

Univariate analysis involves the examination across cases of one variable at a time. There are three major characteristics of a single variable that we tend to look at:

• the distribution
• the central tendency
• the dispersion

In most situations, we would describe all three of these characteristics for each of the variables in our study.

The Distribution

The distribution is a summary of the frequency of individual values or ranges of values for a variable. The simplest distribution would list every value of a variable and the number of persons who had each value. For instance, a typical way to describe the distribution of college students is by year in college, listing the number or percent of students at each of the four years. Or, we describe gender by listing the number or percent of males and females. In these cases, the variable has few enough values that we can list each one and summarize how many sample cases had the value. But what do we do for a variable like income or GPA? With these variables there can be a large number of possible values, with relatively few people having each one. In this case, we group the raw scores into categories according to ranges of values. For instance, we might look at GPA according to the letter grade ranges. Or, we might group income into four or five ranges of income values.

One of the most common ways to describe a single variable is with a frequency distribution . Depending on the particular variable, all of the data values may be represented, or you may group the values into categories first (e.g. with age, price, or temperature variables, it would usually not be sensible to determine the frequencies for each value. Rather, the value are grouped into ranges and the frequencies determined.). Frequency distributions can be depicted in two ways, as a table or as a graph. The table above shows an age frequency distribution with five categories of age ranges defined. The same frequency distribution can be depicted in a graph as shown in Figure 1. This type of graph is often referred to as a histogram or bar chart.

Distributions may also be displayed using percentages. For example, you could use percentages to describe the:

• percentage of people in different income levels
• percentage of people in different age ranges
• percentage of people in different ranges of standardized test scores

Central Tendency

The central tendency of a distribution is an estimate of the “center” of a distribution of values. There are three major types of estimates of central tendency:

The Mean or average is probably the most commonly used method of describing central tendency. To compute the mean all you do is add up all the values and divide by the number of values. For example, the mean or average quiz score is determined by summing all the scores and dividing by the number of students taking the exam. For example, consider the test score values:

The sum of these 8 values is 167 , so the mean is 167/8 = 20.875 .

The Median is the score found at the exact middle of the set of values. One way to compute the median is to list all scores in numerical order, and then locate the score in the center of the sample. For example, if there are 500 scores in the list, score #250 would be the median. If we order the 8 scores shown above, we would get:

There are 8 scores and score #4 and #5 represent the halfway point. Since both of these scores are 20 , the median is 20 . If the two middle scores had different values, you would have to interpolate to determine the median.

The Mode is the most frequently occurring value in the set of scores. To determine the mode, you might again order the scores as shown above, and then count each one. The most frequently occurring value is the mode. In our example, the value 15 occurs three times and is the model. In some distributions there is more than one modal value. For instance, in a bimodal distribution there are two values that occur most frequently.

Notice that for the same set of 8 scores we got three different values ( 20.875 , 20 , and 15 ) for the mean, median and mode respectively. If the distribution is truly normal (i.e. bell-shaped), the mean, median and mode are all equal to each other.

Dispersion refers to the spread of the values around the central tendency. There are two common measures of dispersion, the range and the standard deviation. The range is simply the highest value minus the lowest value. In our example distribution, the high value is 36 and the low is 15 , so the range is 36 - 15 = 21 .

The Standard Deviation is a more accurate and detailed estimate of dispersion because an outlier can greatly exaggerate the range (as was true in this example where the single outlier value of 36 stands apart from the rest of the values. The Standard Deviation shows the relation that set of scores has to the mean of the sample. Again lets take the set of scores:

to compute the standard deviation, we first find the distance between each value and the mean. We know from above that the mean is 20.875 . So, the differences from the mean are:

Notice that values that are below the mean have negative discrepancies and values above it have positive ones. Next, we square each discrepancy:

Now, we take these “squares” and sum them to get the Sum of Squares (SS) value. Here, the sum is 350.875 . Next, we divide this sum by the number of scores minus 1 . Here, the result is 350.875 / 7 = 50.125 . This value is known as the variance . To get the standard deviation, we take the square root of the variance (remember that we squared the deviations earlier). This would be SQRT(50.125) = 7.079901129253 .

Although this computation may seem convoluted, it’s actually quite simple. To see this, consider the formula for the standard deviation:

• X is each score,
• X̄ is the mean (or average),
• n is the number of values,
• Σ means we sum across the values.

In the top part of the ratio, the numerator, we see that each score has the mean subtracted from it, the difference is squared, and the squares are summed. In the bottom part, we take the number of scores minus 1 . The ratio is the variance and the square root is the standard deviation. In English, we can describe the standard deviation as:

the square root of the sum of the squared deviations from the mean divided by the number of scores minus one.

Although we can calculate these univariate statistics by hand, it gets quite tedious when you have more than a few values and variables. Every statistics program is capable of calculating them easily for you. For instance, I put the eight scores into SPSS and got the following table as a result:

which confirms the calculations I did by hand above.

The standard deviation allows us to reach some conclusions about specific scores in our distribution. Assuming that the distribution of scores is normal or bell-shaped (or close to it!), the following conclusions can be reached:

• approximately 68% of the scores in the sample fall within one standard deviation of the mean
• approximately 95% of the scores in the sample fall within two standard deviations of the mean
• approximately 99% of the scores in the sample fall within three standard deviations of the mean

For instance, since the mean in our example is 20.875 and the standard deviation is 7.0799 , we can from the above statement estimate that approximately 95% of the scores will fall in the range of 20.875-(2*7.0799) to 20.875+(2*7.0799) or between 6.7152 and 35.0348 . This kind of information is a critical stepping stone to enabling us to compare the performance of an individual on one variable with their performance on another, even when the variables are measured on entirely different scales.

Cookie Consent

Conjointly uses essential cookies to make our site work. We also use additional cookies in order to understand the usage of the site, gather audience analytics, and for remarketing purposes.

For more information on Conjointly's use of cookies, please read our Cookie Policy .

Which one are you?

I am new to conjointly, i am already using conjointly.

Research Methodology and Descriptive Statistics Course

Dr. Henk van der Kolk

Dr. Lyset Rekes-Mombarg

Blended Learning

You follow this course together with pre-master students of the faculty BMS. We expect that PhD students who register for this course participate actively. Although lectures and tutorials will not be organized for PhD students separately, the teachers will create a separate ‘niche’ where you can meet fellow PhD students. Although participation in lectures, tutorials and discussion boards is not formally required, it is strongly recommended.

Please contact the lecturer for the actual schedule (about 36 sessions in 2 months starting September 2, 2024)

You are signed up for the Course alert

You are now signed up for the course alert. For an overview of all your courses and alerts, see the my courses overview (only for UT employee / student).

• Privacy Policy

Home » Descriptive Research Design – Types, Methods and Examples

Descriptive Research Design – Types, Methods and Examples

Table of Contents

Descriptive research design is a crucial methodology in social sciences, education, healthcare, and business research. It focuses on describing characteristics, behaviors, or phenomena as they exist without influencing or manipulating the study environment. This type of research provides a snapshot of specific conditions or attributes, making it an essential approach for understanding trends, patterns, and relationships.

This article explores the concept of descriptive research design, its types, methods, and practical examples, providing a comprehensive understanding of its significance and applications.

Descriptive Research Design

Descriptive research design is a systematic methodology used to describe the characteristics of a population, event, or phenomenon. Unlike experimental research, which tests hypotheses, descriptive research answers “what,” “where,” “when,” and “how” questions. It does not examine causation but rather provides detailed information about existing conditions.

For example, a study describing the demographics of university students enrolled in online courses would employ a descriptive research design.

Importance of Descriptive Research Design

Descriptive research design is vital for:

• Establishing Baseline Data: It provides foundational knowledge to guide further research.
• Identifying Trends: It captures trends and patterns in behavior or phenomena.
• Informing Decision-Making: Organizations and policymakers rely on descriptive research for data-driven decisions.
• Understanding Complex Phenomena: It helps summarize and explain intricate systems or populations.

This design is widely used in fields such as sociology, psychology, marketing, and healthcare to generate valuable insights.

Types of Descriptive Research Design

1. cross-sectional research.

This type involves collecting data from a population or sample at a single point in time.

• Purpose: To describe the current status or characteristics of a population.
• Example: A survey measuring customer satisfaction with a product conducted in January.

2. Longitudinal Research

Longitudinal research collects data from the same subjects over an extended period, allowing researchers to observe changes and trends.

• Purpose: To identify patterns or changes over time.
• Example: Tracking changes in dietary habits among adolescents over five years.

3. Comparative Research

This design compares two or more groups or phenomena to highlight differences and similarities.

• Purpose: To explore variations and relationships between subjects.
• Example: Comparing stress levels between urban and rural employees.

4. Case Study Research

Case studies provide an in-depth examination of a single subject, group, or event.

• Purpose: To gain detailed insights into complex issues.
• Example: Analyzing the strategies of a successful startup to identify factors contributing to its growth.

Methods of Descriptive Research Design

1. surveys and questionnaires.

Surveys are the most common method in descriptive research, using structured or semi-structured questions to gather data.

• Easy to administer to large populations.
• Cost-effective.
• Example: Conducting a survey to determine customer preferences for smartphone features.

2. Observations

This method involves observing and recording behaviors, events, or conditions without interference.

• Provides real-time, naturalistic data.
• Useful for studying non-verbal behaviors.
• Example: Observing classroom interactions to analyze teacher-student dynamics.

Types of Observations

• Example: Observing a team meeting as a team member.
• Example: Watching interactions from a one-way mirror.

3. Secondary Data Analysis

Analyzing pre-existing data, such as government reports, academic articles, or historical records.

• Saves time and resources.
• Provides access to large datasets.
• Example: Using census data to describe population growth trends.

4. Interviews

Interviews involve asking open-ended or structured questions to gather in-depth information.

• Offers detailed insights and clarifications.
• Facilitates exploration of subjective experiences.
• Example: Conducting interviews with employees to understand workplace satisfaction.

5. Case Studies

Involves a deep dive into a specific instance to understand complex phenomena.

• Provides rich, contextualized data.
• Suitable for unique or rare cases.
• Example: Studying the response of a hospital to a public health emergency.

Steps in Conducting Descriptive Research

Step 1: define the research problem.

Clearly outline what you aim to describe and why it is significant.

• Example: “What are the shopping preferences of millennials in urban areas?”

Step 2: Select the Population or Sample

Identify the group you will study and ensure it represents the target population.

• Example: Randomly selecting 500 participants from an urban demographic.

Step 3: Choose the Data Collection Method

Select the most appropriate method based on the research problem and objectives.

• Example: Using a survey to collect data on customer satisfaction.

Step 4: Gather Data

Administer the survey, conduct interviews, or collect observations systematically.

Step 5: Analyze Data

Summarize findings using statistical or thematic analysis, depending on the nature of the data.

• Quantitative Data: Use statistical tools to identify trends.
• Qualitative Data: Use coding techniques to identify themes.

Step 6: Report Results

Present findings clearly and concisely, often with visuals like graphs, charts, and tables.

Examples of Descriptive Research Design

1. healthcare research.

Study: Assessing patient satisfaction in a hospital.

• Method: Distributing surveys to patients.
• Outcome: Identified areas of improvement in hospital services, such as wait times and staff communication.

2. Marketing Research

Study: Exploring customer preferences for eco-friendly packaging.

• Method: Conducting interviews and focus groups.
• Outcome: Revealed that consumers prefer biodegradable packaging and are willing to pay a premium for it.

3. Education Research

Study: Analyzing attendance patterns among college students.

• Method: Collecting secondary data from attendance records.
• Outcome: Found that attendance declines during midterm weeks, suggesting a need for academic support.

4. Social Research

Study: Examining the impact of social media usage on youth communication skills.

• Method: Observing and surveying participants.
• Outcome: Highlighted that frequent social media use correlates with reduced face-to-face communication skills.

Advantages of Descriptive Research Design

• Easy Implementation: Methods like surveys and observations are straightforward and cost-effective.
• Broad Applications: Can be used across disciplines to gather diverse data.
• Non-Intrusive: Describes phenomena without altering them, preserving natural behavior.
• Rich Data: Provides detailed insights into current states or conditions.

Limitations of Descriptive Research Design

• No Causal Relationships: It does not establish cause-and-effect relationships.
• Bias Potential: Surveys and observations may be subject to bias.
• Limited Scope: Restricted to describing existing conditions, limiting predictive capabilities.

Descriptive research design is an invaluable tool for understanding the characteristics and trends of a population or phenomenon. By employing methods such as surveys, observations, and secondary data analysis, researchers can gather rich, detailed insights that inform decision-making and guide further studies. While it does not explore causation, descriptive research provides a foundation for hypotheses and experimental research, making it a cornerstone of empirical inquiry.

• Creswell, J. W. (2018). Research Design: Qualitative, Quantitative, and Mixed Methods Approaches . Sage Publications.
• Babbie, E. (2020). The Practice of Social Research . Cengage Learning.
• Bryman, A. (2016). Social Research Methods . Oxford University Press.
• Silverman, D. (2020). Interpreting Qualitative Data . Sage Publications.
• Flick, U. (2018). An Introduction to Qualitative Research . Sage Publications.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Experimental Design – Types, Methods, Guide

Quantitative Research – Methods, Types and...

Observational Research – Methods and Guide

Textual Analysis – Types, Examples and Guide

Transformative Design – Methods, Types, Guide

Qualitative Research Methods

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base

Descriptive Statistics | Definitions, Types, Examples

Published on 4 November 2022 by Pritha Bhandari . Revised on 9 January 2023.

Descriptive statistics summarise and organise characteristics of a data set. A data set is a collection of responses or observations from a sample or entire population .

In quantitative research , after collecting data, the first step of statistical analysis is to describe characteristics of the responses, such as the average of one variable (e.g., age), or the relation between two variables (e.g., age and creativity).

The next step is inferential statistics , which help you decide whether your data confirms or refutes your hypothesis and whether it is generalisable to a larger population.

Table of contents

Types of descriptive statistics, frequency distribution, measures of central tendency, measures of variability, univariate descriptive statistics, bivariate descriptive statistics, frequently asked questions.

There are 3 main types of descriptive statistics:

• The distribution concerns the frequency of each value.
• The central tendency concerns the averages of the values.
• The variability or dispersion concerns how spread out the values are.

You can apply these to assess only one variable at a time, in univariate analysis, or to compare two or more, in bivariate and multivariate analysis.

• Go to a library
• Watch a movie at a theater
• Visit a national park

A data set is made up of a distribution of values, or scores. In tables or graphs, you can summarise the frequency of every possible value of a variable in numbers or percentages.

• Simple frequency distribution table
• Grouped frequency distribution table

From this table, you can see that more women than men or people with another gender identity took part in the study. In a grouped frequency distribution, you can group numerical response values and add up the number of responses for each group. You can also convert each of these numbers to percentages.

Measures of central tendency estimate the center, or average, of a data set. The mean , median and mode are 3 ways of finding the average.

Here we will demonstrate how to calculate the mean, median, and mode using the first 6 responses of our survey.

The mean , or M , is the most commonly used method for finding the average.

To find the mean, simply add up all response values and divide the sum by the total number of responses. The total number of responses or observations is called N .

The median is the value that’s exactly in the middle of a data set.

To find the median, order each response value from the smallest to the biggest. Then, the median is the number in the middle. If there are two numbers in the middle, find their mean.

The mode is the simply the most popular or most frequent response value. A data set can have no mode, one mode, or more than one mode.

To find the mode, order your data set from lowest to highest and find the response that occurs most frequently.

Measures of variability give you a sense of how spread out the response values are. The range, standard deviation and variance each reflect different aspects of spread.

The range gives you an idea of how far apart the most extreme response scores are. To find the range , simply subtract the lowest value from the highest value.

Standard deviation

The standard deviation ( s ) is the average amount of variability in your dataset. It tells you, on average, how far each score lies from the mean. The larger the standard deviation, the more variable the data set is.

There are six steps for finding the standard deviation:

• List each score and find their mean.
• Subtract the mean from each score to get the deviation from the mean.
• Square each of these deviations.
• Add up all of the squared deviations.
• Divide the sum of the squared deviations by N – 1.
• Find the square root of the number you found.

Step 5: 421.5/5 = 84.3

Step 6: √84.3 = 9.18

The variance is the average of squared deviations from the mean. Variance reflects the degree of spread in the data set. The more spread the data, the larger the variance is in relation to the mean.

To find the variance, simply square the standard deviation. The symbol for variance is s 2 .

Univariate descriptive statistics focus on only one variable at a time. It’s important to examine data from each variable separately using multiple measures of distribution, central tendency and spread. Programs like SPSS and Excel can be used to easily calculate these.

If you were to only consider the mean as a measure of central tendency, your impression of the ‘middle’ of the data set can be skewed by outliers, unlike the median or mode.

Likewise, while the range is sensitive to extreme values, you should also consider the standard deviation and variance to get easily comparable measures of spread.

If you’ve collected data on more than one variable, you can use bivariate or multivariate descriptive statistics to explore whether there are relationships between them.

In bivariate analysis, you simultaneously study the frequency and variability of two variables to see if they vary together. You can also compare the central tendency of the two variables before performing further statistical tests .

Multivariate analysis is the same as bivariate analysis but with more than two variables.

Contingency table

In a contingency table, each cell represents the intersection of two variables. Usually, an independent variable (e.g., gender) appears along the vertical axis and a dependent one appears along the horizontal axis (e.g., activities). You read ‘across’ the table to see how the independent and dependent variables relate to each other.

Interpreting a contingency table is easier when the raw data is converted to percentages. Percentages make each row comparable to the other by making it seem as if each group had only 100 observations or participants. When creating a percentage-based contingency table, you add the N for each independent variable on the end.

From this table, it is more clear that similar proportions of children and adults go to the library over 17 times a year. Additionally, children most commonly went to the library between 5 and 8 times, while for adults, this number was between 13 and 16.

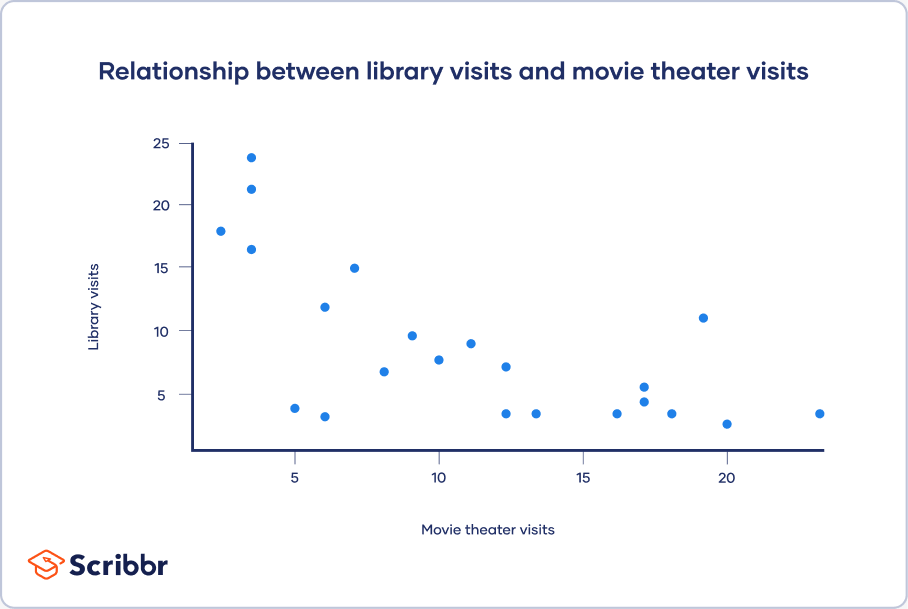
Scatter plots

A scatter plot is a chart that shows you the relationship between two or three variables. It’s a visual representation of the strength of a relationship.

In a scatter plot, you plot one variable along the x-axis and another one along the y-axis. Each data point is represented by a point in the chart.

From your scatter plot, you see that as the number of movies seen at movie theaters increases, the number of visits to the library decreases. Based on your visual assessment of a possible linear relationship, you perform further tests of correlation and regression.

Descriptive statistics summarise the characteristics of a data set. Inferential statistics allow you to test a hypothesis or assess whether your data is generalisable to the broader population.

The 3 main types of descriptive statistics concern the frequency distribution, central tendency, and variability of a dataset.

• Distribution refers to the frequencies of different responses.
• Measures of central tendency give you the average for each response.
• Measures of variability show you the spread or dispersion of your dataset.
• Univariate statistics summarise only one variable  at a time.
• Bivariate statistics compare two variables .
• Multivariate statistics compare more than two variables .

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Bhandari, P. (2023, January 09). Descriptive Statistics | Definitions, Types, Examples. Scribbr. Retrieved 23 December 2024, from https://www.scribbr.co.uk/stats/descriptive-statistics-explained/

Is this article helpful?

Pritha Bhandari

Other students also liked, data collection methods | step-by-step guide & examples, variability | calculating range, iqr, variance, standard deviation, normal distribution | examples, formulas, & uses.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 12: Descriptive Statistics

At this point, we need to consider the basics of data analysis in psychological research in more detail. In this chapter, we focus on descriptive statistics—a set of techniques for summarizing and displaying the data from your sample. We look first at some of the most common techniques for describing single variables, followed by some of the most common techniques for describing statistical relationships between variables. We then look at how to present descriptive statistics in writing and also in the form of tables and graphs that would be appropriate for an American Psychological Association (APA)-style research report. We end with some practical advice for organizing and carrying out your analyses.

Psychology Research Methods Copyright © by The Research Methods Teaching and Learning Group is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book