inductive representation learning on temporal graph

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications You must be signed in to change notification settings

StatsDLMathsRecomSys/Inductive-representation-learning-on-temporal-graphs

Folders and files, repository files navigation, inductive representation learning on temporal graphs (iclr 2020), authors: da xu*, chuanwei ruan*, sushant kumar, evren korpeoglu, kannan achan, please contact [email protected] or [email protected] for questions., follow-up work:.

• A Temporal Kernel Approach for Deep Learning with Continuous-time Information, ICLR 2021 ( https://arxiv.org/abs/2103.15213 )

Predecessor work:

• Self-attention with Functional Time Representation Learning, NeurIPS 2019 ( https://arxiv.org/abs/1911.12864 )

Introduction

The evolving nature of temporal dynamic graphs requires handling new nodes as well as capturing temporal patterns. The node embeddings, as functions of time, should represent both the static node features and the evolving topological structures.

We propose the temporal graph attention (TGAT) layer to efficiently aggregate temporal-topological neighborhood features as well as to learn the time-feature interactions. Stacking TGAT layers, the network recognizes the node embeddings as functions of time and is able to inductively infer embeddings for both new and observed nodes as the graph evolves.

The proposed approach handles both node classification and link prediction task, and can be naturally extended to include the temporal edge features.

Paper link: Inductive Representation Learning on Temporal Graphs

Self-attention with functional representation learning

The theoretical arguments developed in this paper are from our concurrent work: Self-attention with Functional Time Representation Learning (NeurIPS 2019) . The implementation is also available at the github page .

Running the experiments

Dataset and preprocessing, download the public data, preprocess the data.

We use the dense npy format to save the features in binary format. If edge features or nodes features are absent, it will be replaced by a vector of zeros.

Use your own data

Put your data under processed folder. The required input data includes ml_${DATA_NAME}.csv , ml_${DATA_NAME}.npy and ml_${DATA_NAME}_node.npy . They store the edge linkages, edge features and node features respectively.

The CSV file has following columns

, which represents source node index, target node index, time stamp, edge label and the edge index.

ml_${DATA_NAME}.npy has shape of [#temporal edges + 1, edge features dimention]. Similarly, ml_${DATA_NAME}_node.npy has shape of [#nodes + 1, node features dimension].

All node index starts from 1 . The zero index is reserved for null during padding operations. So the maximum of node index equals to the total number of nodes. Similarly, maxinum of edge index equals to the total number of temporal edges. The padding embeddings or the null embeddings is a vector of zeros.

Requirements

python >= 3.7

Command and configurations

Sample commend.

• Learning the network using link prediction tasks
• Learning the down-stream task (node-classification)

Node-classification task reuses the network trained previously. Make sure the prefix is the same so that the checkpoint can be found under saved_models .

General flags

• Python 100.0%

Inductive representation learning on temporal graphs

Da xu , chuanwei ruan , evren korpeoglu , sushant kumar , kannan achan.

Keywords: attention , graph embedding , representation learning , self attention

Abstract: Inductive representation learning on temporal graphs is an important step toward salable machine learning on real-world dynamic networks. The evolving nature of temporal dynamic graphs requires handling new nodes as well as capturing temporal patterns. The node embeddings, which are now functions of time, should represent both the static node features and the evolving topological structures. Moreover, node and topological features can be temporal as well, whose patterns the node embeddings should also capture. We propose the temporal graph attention (TGAT) layer to efficiently aggregate temporal-topological neighborhood features to learn the time-feature interactions. For TGAT, we use the self-attention mechanism as building block and develop a novel functional time encoding technique based on the classical Bochner's theorem from harmonic analysis. By stacking TGAT layers, the network recognizes the node embeddings as functions of time and is able to inductively infer embeddings for both new and observed nodes as the graph evolves. The proposed approach handles both node classification and link prediction task, and can be naturally extended to include the temporal edge features. We evaluate our method with transductive and inductive tasks under temporal settings with two benchmark and one industrial dataset. Our TGAT model compares favorably to state-of-the-art baselines as well as the previous temporal graph embedding approaches.

Similar Papers

On the equivalence between positional node embeddings and structural graph representations, balasubramaniam srinivasan, bruno ribeiro,.

Graph inference learning for semi-supervised classification

Chunyan xu, zhen cui, xiaobin hong, tong zhang, jian yang, wei liu,.

GraphZoom: A Multi-level Spectral Approach for Accurate and Scalable Graph Embedding

Chenhui deng, zhiqiang zhao, yongyu wang, zhiru zhang, zhuo feng,.

Inductive representation learning on temporal graphs

Inductive representation learning on temporal graphs is an important step toward salable machine learning on real-world dynamic networks. The evolving nature of temporal dynamic graphs requires handling new nodes as well as capturing temporal patterns. The node embeddings, which are now functions of time, should represent both the static node features and the evolving topological structures. Moreover, node and topological features can be temporal as well, whose patterns the node embeddings should also capture. We propose the temporal graph attention (TGAT) layer to efficiently aggregate temporal-topological neighborhood features as well as to learn the time-feature interactions. For TGAT, we use the self-attention mechanism as building block and develop a novel functional time encoding technique based on the classical Bochner’s theorem from harmonic alaysis. By stacking TGAT layers, the network recognizes the node embeddings as functions of time and is able to inductively infer embeddings for both new and observed nodes as the graph evolves. The proposed approach handles both node classification and link prediction task, and can be naturally extended to include the temporal edge features. We evaluate our method with transductive and inductive tasks under temporal settings with two benchmark and one industrial dataset. Our TGAT model compares favorably to state-of-the-art baselines as well as the previous temporal graph embedding approaches.

1 Introduction

The technique of learning lower-dimensional vector embeddings on graphs have been widely applied to graph analysis tasks (Perozzi et al., 2014 ; Tang et al., 2015 ; Wang et al., 2016 ) and deployed in industrial systems (Ying et al., 2018 ; Wang et al., 2018a ) . Most of the graph representation learning approaches only accept static or non-temporal graphs as input, despite the fact that many graph-structured data are time-dependent. In social network, citation network, question answering forum and user-item interaction system, graphs are created as temporal interactions between nodes. Using the final state as a static portrait of the graph is reasonable in some cases, such as the protein-protein interaction network, as long as node interactions are timeless in nature. Otherwise, ignoring the temporal information can severely diminish the modelling efforts and even causing questionable inference. For instance, models may mistakenly utilize future information for predicting past interactions during training and testing if the temporal constraints are disregarded. More importantly, the dynamic and evolving nature of many graph-related problems demand an explicitly modelling of the timeliness whenever nodes and edges are added, deleted or changed over time.

Learning representations on temporal graphs is extremely challenging, and it is not until recently that several solutions are proposed (Nguyen et al., 2018 ; Li et al., 2018 ; Goyal et al., 2018 ; Trivedi et al., 2018 ) . We conclude the challenges in three folds. Firstly , to model the temporal dynamics, node embeddings should not be only the projections of topological structures and node features but also functions of the continuous time. Therefore, in addition to the usual vector space, temporal representation learning should be operated in some functional space as well. Secondly , graph topological structures are no longer static since the nodes and edges are evolving over time, which poses temporal constraints on neighborhood aggregation methods. Thirdly , node features and topological structures can exhibit temporal patterns. For example, node interactions that took place long ago may have less impact on the current topological structure and thus the node embeddings. Also, some nodes may possess features that allows them having more regular or recurrent interactions with others. We provide sketched plots for visual illustration in Figure 1 .

Similar to its non-temporal counterparts, in the real-world applications, models for representation learning on temporal graphs should be able to quickly generate embeddings whenever required, in an inductive fashion. GraphSAGE (Hamilton et al., 2017a ) and graph attention network ( GAT ) (Veličković et al., 2017 ) are capable of inductively generating embeddings for unseen nodes based on their features, however, they do not consider the temporal factors. Most of the temporal graph embedding methods can only handle transductive tasks, since they require re-training or the computationally-expensive gradient calculations to infer embeddings for unseen nodes or node embeddings for a new timepoint. In this work, we aim at developing an architecture to inductively learn representations for temporal graphs such that the time-aware embeddings (for unseen and observed nodes) can be obtained via a single network forward pass. The key to our approach is the combination of the self-attention mechanism (Vaswani et al., 2017 ) and a novel functional time encoding technique derived from the Bochner’s theorem from classical harmonic analysis (Loomis, 2013 ) .

The motivation for adapting self-attention to inductive representation learning on temporal graphs is to identify and capture relevant pieces of the temporal neighborhood information. Both graph convolutional network ( GCN ) (Kipf & Welling, 2016a ) and GAT are implicitly or explicitly assigning different weights to neighboring nodes (Veličković et al., 2017 ) when aggregating node features. The self-attention mechanism was initially designed to recognize the relevant parts of input sequence in natural language processing. As a discrete-event sequence learning method, self-attention outputs a vector representation of the input sequence as a weighted sum of individual entry embeddings. Self-attention enjoys several advantages such as parallelized computation and interpretability (Vaswani et al., 2017 ) . Since it captures sequential information only through the positional encoding, temporal features can not be handled. Therefore, we are motivated to replace positional encoding with some vector representation of time. Since time is a continuous variable, the mapping from the time domain to vector space has to be functional. We gain insights from harmonic analysis and propose a theoretical-grounded functional time encoding approach that is compatible with the self-attention mechanism. The temporal signals are then modelled by the interactions between the functional time encoding and nodes features as well as the graph topological structures.

To evaluate our approach, we consider future link prediction on the observed nodes as transductive learning task, and on the unseen nodes as inductive learning task. We also examine the dynamic node classification task using node embeddings (temporal versus non-temporal) as features to demonstrate the usefulness of our functional time encoding. We carry out extensive ablation studies and sensitivity analysis to show the effectiveness of the proposed functional time encoding and TGAT -layer.

2 Related Work

Graph representation learning . Spectral graph embedding models operate on the graph spectral domain by approximating, projecting or expanding the graph Laplacian (Kipf & Welling, 2016a ; Henaff et al., 2015 ; Defferrard et al., 2016 ) . Since their training and inference are conditioned on the specific graph spectrum, they are not directly extendable to temporal graphs. Non-spectral approaches, such as GAT , GraphSAGE and MoNET , (Monti et al., 2017 ) rely on the localized neighbourhood aggregations and thus are not restricted to the training graph. GraphSAGE and GAT also have the flexibility to handle evolving graphs inductively. To extend classical graph representation learning approaches to the temporal domain, several attempts have been done by cropping the temporal graph into a sequence of graph snapshots (Li et al., 2018 ; Goyal et al., 2018 ; Rahman et al., 2018 ; Xu et al., 2019b ) , and some others work with temporally persistent node (edges) (Trivedi et al., 2018 ; Ma et al., 2018 ) . Nguyen et al. ( 2018 ) proposes a node embedding method based on temporal random walk and reported state-of-the-art performances. However, their approach only generates embeddings for the final state of temporal graph and can not directly apply to the inductive setting.

Self-attention mechanism. Self-attention mechanisms often have two components: the embedding layer and the attention layer. The embedding layer takes an ordered entity sequence as input. Self-attention uses the positional encoding, i.e. each position k 𝑘 k is equipped with a vector 𝐩 k subscript 𝐩 𝑘 \mathbf{p}_{k} (fixed or learnt) which is shared for all sequences. For the entity sequence 𝐞 = ( e 1 , … , e l ) 𝐞 subscript 𝑒 1 … subscript 𝑒 𝑙 \mathbf{e}=(e_{1},\ldots,e_{l}) , the embedding layer takes the sum or concatenation of entity embeddings (or features) ( 𝐳 ∈ ℝ d 𝐳 superscript ℝ 𝑑 \mathbf{z}\in\mathbb{R}^{d} ) and their positional encodings as input:

where | | || denotes concatenation operation and d pos subscript 𝑑 pos d_{\text{pos}} is the dimension for positional encoding. Self-attention layers can be constructed using the scaled dot-product attention, which is defined as:

where 𝐐 𝐐 \mathbf{Q} denotes the ’queries’, 𝐊 𝐊 \mathbf{K} the ’keys’ and 𝐕 𝐕 \mathbf{V} the ’values’. In Vaswani et al. ( 2017 ) , they are treated as projections of the output 𝐙 𝐞 subscript 𝐙 𝐞 \mathbf{Z}_{\mathbf{e}} : 𝐐 = 𝐙 𝐞 ​ 𝐖 Q , 𝐊 = 𝐙 𝐞 ​ 𝐖 K , 𝐕 = 𝐙 𝐞 ​ 𝐖 V , formulae-sequence 𝐐 subscript 𝐙 𝐞 subscript 𝐖 𝑄 formulae-sequence 𝐊 subscript 𝐙 𝐞 subscript 𝐖 𝐾 𝐕 subscript 𝐙 𝐞 subscript 𝐖 𝑉 \mathbf{Q}=\mathbf{Z}_{\mathbf{e}}\mathbf{W}_{Q},\quad\mathbf{K}=\mathbf{Z}_{\mathbf{e}}\mathbf{W}_{K},\quad\mathbf{V}=\mathbf{Z}_{\mathbf{e}}\mathbf{W}_{V}, where 𝐖 Q subscript 𝐖 𝑄 \mathbf{W}_{Q} , 𝐖 K subscript 𝐖 𝐾 \mathbf{W}_{K} and 𝐖 V subscript 𝐖 𝑉 \mathbf{W}_{V} are the projection matrices. Since each row of 𝐐 𝐐 \mathbf{Q} , 𝐊 𝐊 \mathbf{K} and 𝐕 𝐕 \mathbf{V} represents an entity, the dot-product attention takes a weighted sum of the entity ’values’ in 𝐕 𝐕 \mathbf{V} where the weights are given by the interactions of entity ’query-key’ pairs. The hidden representation for the entity sequence under the dot-product attention is then given by h 𝐞 = Attn ​ ( 𝐐 , 𝐊 , 𝐕 ) subscript ℎ 𝐞 Attn 𝐐 𝐊 𝐕 h_{\mathbf{e}}=\text{Attn}(\mathbf{Q},\mathbf{K},\mathbf{V}) .

3 Temporal Graph Attention Network Architecture

We first derive the mapping from time domain to the continuous differentiable functional domain as the functional time encoding such that resulting formulation is compatible with self-attention mechanism as well as the backpropagation-based optimization frameworks. The same idea was explored in a concurrent work (Xu et al., 2019a ) . We then present the temporal graph attention layer and show how it can be naturally extended to incorporate the edge features.

3.1 Functional time encoding

subscript 𝑡 2 𝑐 𝜓 subscript 𝑡 1 subscript 𝑡 2 𝒦 subscript 𝑡 1 subscript 𝑡 2 \mathcal{K}(t_{1}+c,t_{2}+c)=\psi(t_{1}-t_{2})=\mathcal{K}(t_{1},t_{2}) for any constant c 𝑐 c . Generally speaking, functional learning is extremely complicated since it operates on infinite-dimensional spaces, but now we have transformed the problem into learning the temporal kernel 𝒦 𝒦 \mathcal{K} expressed by Φ Φ \Phi . Nonetheless, we still need to figure out an explicit parameterization for Φ Φ \Phi in order to conduct efficient gradient-based optimization. Classical harmonic analysis theory, i.e. the Bochner’s theorem, motivates our final solution. We point out that the temporal kernel 𝒦 𝒦 \mathcal{K} is positive-semidefinite (PSD) and continuous, since it is defined via Gram matrix and the mapping Φ Φ \Phi is continuous. Therefore, the kernel 𝒦 𝒦 \mathcal{K} defined above satisfy the assumptions of the Bochner’s theorem, which we state below.

Theorem 1 (Bochner’s Theorem) .

A continuous, translation-invariant kernel 𝒦 ​ ( 𝐱 , 𝐲 ) = ψ ​ ( 𝐱 − 𝐲 ) 𝒦 𝐱 𝐲 𝜓 𝐱 𝐲 \mathcal{K}(\mathbf{x},\mathbf{y})=\psi(\mathbf{x}-\mathbf{y}) on ℝ d superscript ℝ 𝑑 \mathbb{R}^{d} is positive definite if and only if there exists a non-negative measure on ℝ ℝ \mathbb{R} such that ψ 𝜓 \psi is the Fourier transform of the measure.

Consequently, when scaled properly, our temporal kernel 𝒦 𝒦 \mathcal{K} have the alternate expression:

where ξ ω ​ ( t ) = e i ​ ω ​ t subscript 𝜉 𝜔 𝑡 superscript 𝑒 𝑖 𝜔 𝑡 \xi_{\omega}(t)=e^{i\omega t} . Since the kernel 𝒦 𝒦 \mathcal{K} and the probability measure p ​ ( ω ) 𝑝 𝜔 p(\omega) are real, we extract the real part of ( 3 ) and obtain:

Let p ​ ( ω ) 𝑝 𝜔 p(\omega) be the corresponding probability measure stated in Bochner’s Theorem for kernel function 𝒦 𝒦 \mathcal{K} . Suppose the feature map Φ Φ \Phi is constructed as described above using samples { ω i } i = 1 d superscript subscript subscript 𝜔 𝑖 𝑖 1 𝑑 \{\omega_{i}\}_{i=1}^{d} , then we only need d = Ω ​ ( 1 ϵ 2 ​ log ⁡ σ p 2 ​ t max ϵ ) 𝑑 Ω 1 superscript italic-ϵ 2 superscript subscript 𝜎 𝑝 2 subscript 𝑡 italic-ϵ d=\Omega\big{(}\frac{1}{\epsilon^{2}}\log\frac{\sigma_{p}^{2}t_{\max}}{\epsilon}\big{)} samples to have

where σ p 2 superscript subscript 𝜎 𝑝 2 \sigma_{p}^{2} is the second momentum with respect to p ​ ( ω ) 𝑝 𝜔 p(\omega) .

The proof is provided in supplement material.

By applying Bochner’s theorem, we convert the problem of kernel learning to distribution learning, i.e. estimating the p ​ ( ω ) 𝑝 𝜔 p(\omega) in Theorem 1. A straightforward solution is to apply the reparameterization trick by using auxiliary random variables with a known marginal distribution as in variational autoencoders (Kingma & Welling, 2013 ) . However, the reparameterization trick is often limited to certain distributions such as the ’local-scale’ family, which may not be rich enough for our purpose. For instance, when p ​ ( ω ) 𝑝 𝜔 p(\omega) is multimodal it is difficult to reconstruct the underlying distribution via direct reparameterizations. An alternate approach is to use the inverse cumulative distribution function (CDF) transformation. Rezende & Mohamed ( 2015 ) propose using parameterized normalizing flow , i.e. a sequence of invertible transformation functions, to approximate arbitrarily complicated CDF and efficiently sample from it. Dinh et al. ( 2016 ) further considers stacking bijective transformations, known as affine coupling layer, to achieve more effective CDF estimation. The above methods learns the inverse CDF function F θ − 1 ( . ) F^{-1}_{\theta}(.) parameterized by flow-based networks and draw samples from the corresponding distribution. On the other hand, if we consider an non-parameterized approach for estimating distribution, then learning F − 1 ( . ) F^{-1}(.) and obtain d 𝑑 d samples from it is equivalent to directly optimizing the { ω 1 , … , ω d } subscript 𝜔 1 … subscript 𝜔 𝑑 \{\omega_{1},\ldots,\omega_{d}\} in ( 4 ) as free model parameters. In practice, we find these two approaches to have highly comparable performances (see supplement material). Therefore we focus on the non-parametric approach, since it is more parameter-efficient and has faster training speed (as no sampling during training is required).

The above functional time encoding is fully compatible with self-attention, thus they can replace the positional encodings in ( 1 ) and their parameters are jointly optimized as part of the whole model.

3.2 Temporal graph attention layer

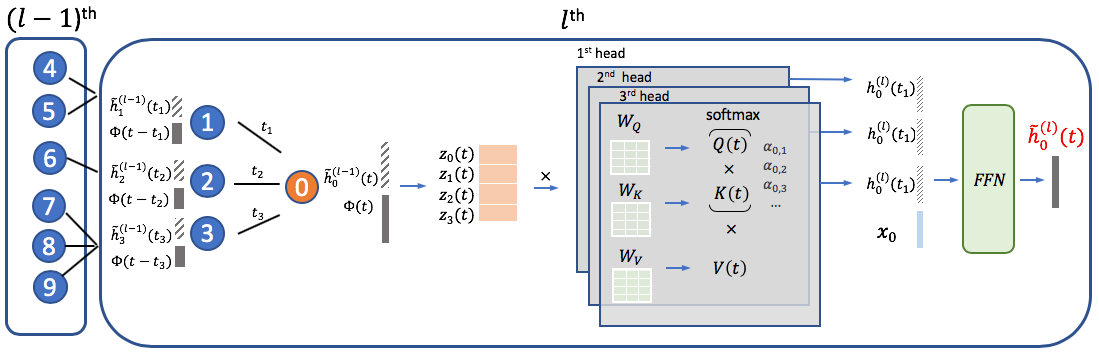
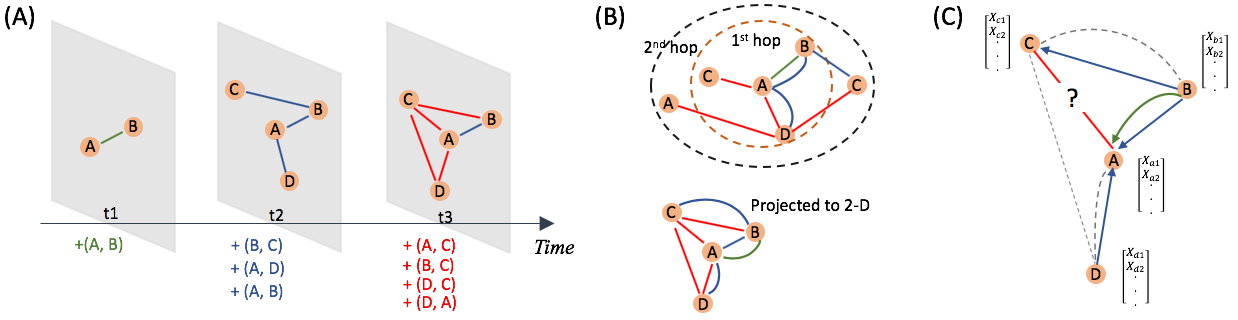
We use v i subscript 𝑣 𝑖 v_{i} and 𝐱 i ∈ ℝ d 0 subscript 𝐱 𝑖 superscript ℝ subscript 𝑑 0 \mathbf{x}_{i}\in\mathbb{R}^{d_{0}} to denote node i 𝑖 i and its raw node features. The proposed TGAT architecture depends solely on the temporal graph attention layer ( TGAT layer). In analogy to GraphSAGE and GAT , the TGAT layer can be thought of as a local aggregation operator that takes the temporal neighborhood with their hidden representations (or features) as well as timestamps as input, and the output is the time-aware representation for target node at any time point t 𝑡 t . We denote the hidden representation output for node i 𝑖 i at time t 𝑡 t from the l t ​ h superscript 𝑙 𝑡 ℎ l^{th} layer as 𝐡 ~ i ( l ) ​ ( t ) subscript superscript ~ 𝐡 𝑙 𝑖 𝑡 \tilde{\mathbf{h}}^{(l)}_{i}(t) .

In line with original self-attention mechanism, we first obtain the entity-temporal feature matrix as

and forward it to three different linear projections to obtain the ’query’, ’key’ and ’value’:

To combine neighbourhood representation with the target node features, we adopt the same practice from GraphSAGE and concatenate the neighbourhood representation with the target node’s feature vector 𝐳 0 subscript 𝐳 0 \mathbf{z}_{0} . We then pass it to a feed-forward neural network to capture non-linear interactions between the features as in (Vaswani et al., 2017 ) :

where 𝐡 ~ 0 ( l ) ​ ( t ) ∈ ℝ d subscript superscript ~ 𝐡 𝑙 0 𝑡 superscript ℝ 𝑑 \tilde{\mathbf{h}}^{(l)}_{0}(t)\in\mathbb{R}^{d} is the final output representing the time-aware node embedding at time t 𝑡 t for the target node. Therefore, the TGAT layer can be implemented for node classification task using the semi-supervised learning framework proposed in Kipf & Welling ( 2016a ) as well as the link prediction task with the encoder-decoder framework summarized by Hamilton et al. ( 2017b ) .

Just like GraphSAGE , a single TGAT layer aggregates the localized one-hop neighborhood, and by stacking L 𝐿 L TGAT layers the aggregation extends to L 𝐿 L hops. Similar to GAT , out approach does not restrict the size of neighborhood. We provide a graphical illustration of our TGAT layer in Figure 2 .

3.3 Extension to incorporate Edge Features

such that the edge information is propagated to the target node’s hidden representation, and then passed on to the next layer (if exists). The remaining structures stay the same as in Section 3.2 .

3.4 Temporal sub-graph batching

Stacking L 𝐿 L TGAT layers is equivalent to aggregate over the L 𝐿 L -hop neighborhood. For each L 𝐿 L -hop sub-graph that is constructed during the batch-wise training, all message passing directions must be aligned with the observed chronological orders. Unlike the non-temporal setting where each edge appears only once, in temporal graphs two node can have multiple interactions at different time points. Whether or not to allow loops that involve the target node should be judged case-by-case. Sampling from neighborhood, or known as neighborhood dropout , may speed up and stabilize model training. For temporal graphs, neighborhood dropout can be carried uniformly or weighted by the inverse timespan such that more recent interactions has higher probability of being sampled.

3.5 Comparisons to related work

The functional time encoding technique and TGAT layer introduced in Section 3.1 and 3.2 solves several critical challenges, and the TGAT network intrinsically connects to several prior methods.

Instead of cropping temporal graphs into a sequence of snapshots or constructing time-constraint random walks, which inspired most of the current temporal graph embedding methods, we directly learn the functional representation of time. The proposed approach is motivated by and thus fully compatible with the well-established self-attention mechanism. Also, to the best of our knowledge, no previous work has discussed the temporal-feature interactions for temporal graphs, which is also considered in our approach.

The TGAT layer is computationally efficient compared with RNN-based models, since the masked self-attention operation is parallelizable, as suggested by Vaswani et al. ( 2017 ) . The per-batch time complexity of the TGAT layer with k 𝑘 k heads and l 𝑙 l layers can be expressed as O ​ ( ( k ​ N ~ ) l ) 𝑂 superscript 𝑘 ~ 𝑁 𝑙 O\big{(}(k\tilde{N})^{l}\big{)} where N ~ ~ 𝑁 \tilde{N} is the average neighborhood size, which is comparable to GAT . When using multi-head attention, the computation for each head can be parallelized as well.

The inference with TGAT is entirely inductive . With an explicit functional expression h ~ ​ ( t ) ~ ℎ 𝑡 \tilde{h}(t) for each node, the time-aware node embeddings can be easily inferred for any timestamp via a single network forward pass. Similarity, whenever the graph is updated, the embeddings for both unseen and observed nodes can be quickly inferred in an inductive fashion similar to that of GraphSAGE , and the computations can be parallelized across all nodes.

GraphSAGE with mean pooling (Hamilton et al., 2017a ) can be interpreted as a special case of the proposed method, where the temporal neighborhood is aggregated with equal attention coefficients. GAT is like the time-agnostic version of our approach but with a different formulation for self-attention, as they refer to the work of Bahdanau et al. ( 2014 ) . We discuss the differences in detail in the Appendix. It is also straightforward to show our connections with the menory networks (Sukhbaatar et al., 2015 ) by thinking of the temporal neighborhoods as memory. The techniques developed in our work may also help adapting GAT and GraphSAGE to temporal settings as we show in our experiments.

4 Experiment and Results

We test the performance of the proposed method against a variety of strong baselines (adapted for temporal settings when possible) and competing approaches, for both the inductive and transductive tasks on two benchmark and one large-scale industrial dataset.

4.1 Datasets

Real-world temporal graphs consist of time-sensitive node interactions, evolving node labels as well as new nodes and edges. We choose the following datasets which contain all scenarios.

Reddit dataset . 2 2 2 http://snap.stanford.edu/jodie/reddit.csv We use the data from active users and their posts under subreddits, leading to a temporal graph with 11,000 nodes, ∼ similar-to \sim 700,000 temporal edges and dynamic labels indicating whether a user is banned from posting. The user posts are transformed into edge feature vectors.

Wikipedia dataset . 3 3 3 http://snap.stanford.edu/jodie/wikipedia.csv We use the data from top edited pages and active users, yielding a temporal graph ∼ similar-to \sim 9,300 nodes and around 160,000 temporal edges. Dynamic labels indicate if users are temporarily banned from editing. The user edits are also treated as edge features.

Industrial dataset . We choose 70,000 popular products and 100,000 active customers as nodes from the online grocery shopping website 4 4 4 https://grocery.walmart.com/ and use the customer-product purchase as temporal edges ( ∼ similar-to \sim 2 million). The customers are tagged with labels indicating if they have a recent interest in dietary products. Product features are given by the pre-trained product embeddings (Xu et al., 2020 ) .

We do the chronological train-validation-test split with 70%-15%-15% according to node interaction timestamps. The dataset and preprocessing details are provided in the supplement material.

4.2 Transductive and inductive learning tasks

Since the majority of temporal information is reflected via the timely interactions among nodes, we choose to use a more revealing link prediction setup for training. Node classification is then treated as the downstream task using the obtained time-aware node embeddings as input.

Transductive task examines embeddings of the nodes that have been observed in training, via the future link prediction task and the node classification. To avoid violating temporal constraints, we predict the links that strictly take place posterior to all observations in the training data.

Inductive task examines the inductive learning capability using the inferred representations of unseen nodes, by predicting the future links between unseen nodes and classify them based on their inferred embedding dynamically. We point out that it suffices to only consider the future sub-graph for unseen nodes since they are equivalent to new graphs under the non-temporal setting.

As for the evaluation metrics , in the link prediction tasks, we first sample an equal amount of negative node pairs to the positive links and then compute the average precision ( AP ) and classification accuracy . In the downstream node classification tasks, due to the label imbalance in the datasets, we employ the area under the ROC curve ( AUC ).

4.3 Baselines

Transductive task : for link prediction of observed nodes, we choose the compare our approach with the state-of-the-art graph embedding methods: GAE and VGAE (Kipf & Welling, 2016b ) . For complete comparisons, we also include the skip-gram-based node2vec (Grover & Leskovec, 2016 ) as well as the spectral-based DeepWalk model (Perozzi et al., 2014 ) , using the same inner-product decoder as GAE for link prediction. The CDTNE model based on the temporal random walk has been reported with superior performance on transductive learning tasks (Nguyen et al., 2018 ) , so we include CDTNE as the representative for temporal graph embedding approaches.

Inductive task : few approaches are capable of managing inductive learning on graphs even in the non-temporal setting. As a consequence, we choose GraphSAGE and GAT as baselines after adapting them to the temporal setting. In particular, we equip them with the same temporal sub-graph batching describe in Section 3.4 to maximize their usage on temporal information. Also, we implement the extended version for the baselines to include edge features in the same way as ours (in Section 3.3 ). We experiment on different aggregation functions for GraphSAGE , i.e. GraphSAGE -mean, GraphSAGE -pool and GraphSAGE -LSTM. In accordance with the original work of Hamilton et al. ( 2017a ) , GraphSAGE -LSTM gives the best validation performance among the three approaches, which is reasonable under temporal setting since LSTM aggregation takes account of the sequential information. Therefore we report the results of GraphSAGE -LSTM.

In addition to the above baselines, we implement a version of TGAT with all temporal attention weights set to equal value ( Const-TGAT ). Finally, to show that the superiority of our approach owes to both the time encoding and the network architecture, we experiment with the enhanced GAT and GraphSAGE -mean by concatenating the proposed time encoding to the original features during temporal aggregations ( GAT+T and GraphSAGE+T ).

4.4 Experiment setup

We use the time-sensitive link prediction loss function for training the l 𝑙 l -layer TGAT network:

subscript 𝑑 ℎ subscript 𝑑 0 subscript 𝑑 𝑓 subscript 𝑑 𝑓 𝑑 \Omega\big{(}(d+d_{T})d_{h}+(d_{h}+d_{0})d_{f}+d_{f}d\big{)} parameters for each attention head, which is independent of the graph and neighborhood size. Using two TGAT layers and two attention heads with dropout rate as 0.1 give the best validation performance. For inference, we inductively compute the embeddings for both the unseen and observed nodes at each time point that the graph evolves, or when the node labels are updated. We then use these embeddings as features for the future link prediction and dynamic node classifications with multilayer perceptron.

We further conduct ablation study to demonstrate the effectiveness of the proposed functional time encoding approach. We experiment on abandoning time encoding or replacing it with the original positional encoding (both fixed and learnt). We also compare the uniform neighborhood dropout to sampling with inverse timespan (where the recent edges are more likely to be sampled), which is provided in supplement material along with other implementation details and setups for baselines.

4.5 Results

The results in Table 1 and Table 2 demonstrates the state-of-the-art performances of our approach on both transductive and inductive learning tasks. In the inductive learning task, our TGAT network significantly improves upon the the upgraded GraphSAGE -LSTM and GAT in accuracy and average precision by at least 5 % for both metrics, and in the transductive learning task TGAT consistently outperforms all baselines across datasets. While GAT+T and GraphSAGE+T slightly outperform or tie with GAT and GraphSAGE -LSTM, they are nevertheless outperformed by our approach. On one hand, the results suggest that the time encoding have potential to extend non-temporal graph representation learning methods to temporal settings. On the other, we note that the time encoding still works the best with our network architecture which is designed for temporal graphs. Overall, the results demonstrate the superiority of our approach in learning representations on temporal graphs over prior models. We also see the benefits from assigning temporal attention weights to neighboring nodes, where GAT significantly outperforms the Const-TGAT in all three tasks. The dynamic node classification outcome (in Table 3 ) further suggests the usefulness of our time-aware node embeddings for downstream tasks as they surpass all the baselines. The ablation study results of Figure 3 successfully reveals the effectiveness of the proposed functional time encoding approach in capturing temporal signals as it outperforms the positional encoding counterparts.

4.6 Attention Analysis

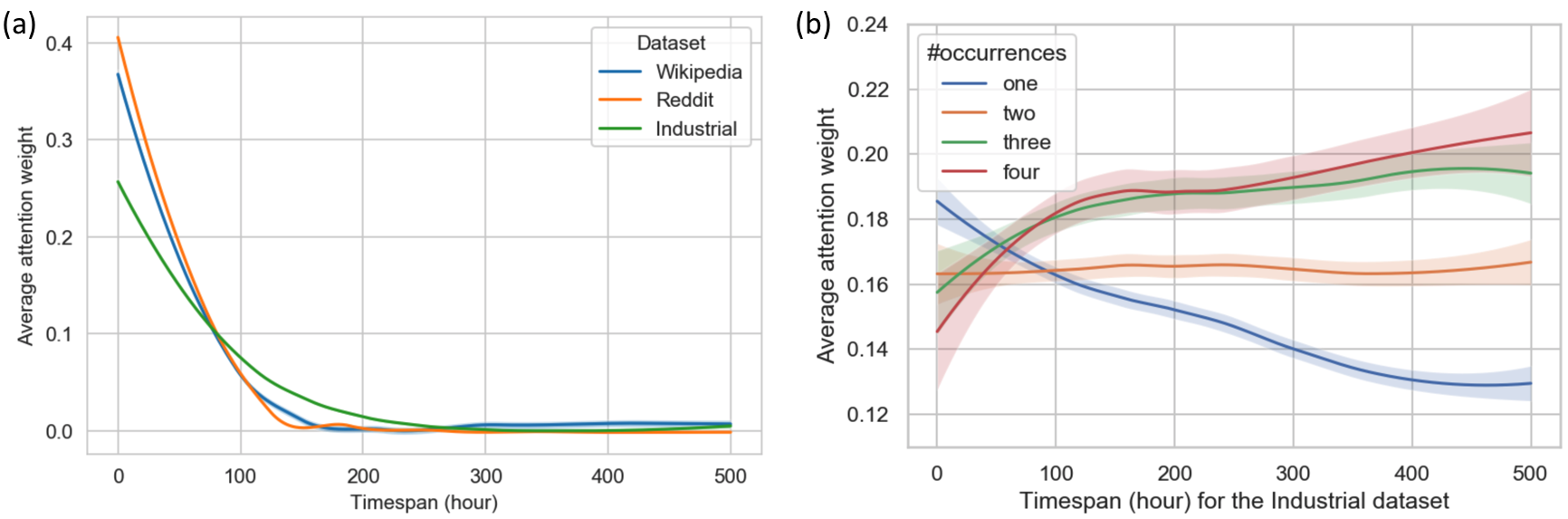
5 Conclusion and future work

We introduce a novel time-aware graph attention network for inductive representation learning on temporal graphs. We adapt the self-attention mechanism to handle the continuous time by proposing a theoretically-grounded functional time encoding. Theoretical and experimental analysis demonstrate the effectiveness of our approach for capturing temporal-feature signals in terms of both node and topological features on temporal graphs. Self-attention mechanism often provides useful model interpretations (Vaswani et al., 2017 ) , which is an important direction of our future work. Developing tools to visualize the evolving graph dynamics and temporal representations efficiently is another important direction for both research and application. Also, the functional time encoding technique has huge potential for adapting other deep learning methods to the temporal graph domain.

• Bahdanau et al. (2014) Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473 , 2014.
• Battaglia et al. (2018) Peter W Battaglia, Jessica B Hamrick, Victor Bapst, Alvaro Sanchez-Gonzalez, Vinicius Zambaldi, Mateusz Malinowski, Andrea Tacchetti, David Raposo, Adam Santoro, Ryan Faulkner, et al. Relational inductive biases, deep learning, and graph networks. arXiv preprint arXiv:1806.01261 , 2018.
• Defferrard et al. (2016) Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in neural information processing systems , pp. 3844–3852, 2016.
• Dinh et al. (2016) Laurent Dinh, Jascha Sohl-Dickstein, and Samy Bengio. Density estimation using real nvp. arXiv preprint arXiv:1605.08803 , 2016.
• Fey & Lenssen (2019) Matthias Fey and Jan E. Lenssen. Fast graph representation learning with PyTorch Geometric. In ICLR Workshop on Representation Learning on Graphs and Manifolds , 2019.
• Goyal et al. (2018) Palash Goyal, Nitin Kamra, Xinran He, and Yan Liu. Dyngem: Deep embedding method for dynamic graphs. arXiv preprint arXiv:1805.11273 , 2018.
• Grover & Leskovec (2016) Aditya Grover and Jure Leskovec. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining , pp.  855–864. ACM, 2016.
• Hamilton et al. (2017a) Will Hamilton, Zhitao Ying, and Jure Leskovec. Inductive representation learning on large graphs. In Advances in Neural Information Processing Systems , pp. 1024–1034, 2017a.
• Hamilton et al. (2017b) William L Hamilton, Rex Ying, and Jure Leskovec. Representation learning on graphs: Methods and applications. arXiv preprint arXiv:1709.05584 , 2017b.
• Henaff et al. (2015) Mikael Henaff, Joan Bruna, and Yann LeCun. Deep convolutional networks on graph-structured data. arXiv preprint arXiv:1506.05163 , 2015.
• Kingma & Welling (2013) Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114 , 2013.
• Kipf & Welling (2016a) Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907 , 2016a.
• Kipf & Welling (2016b) Thomas N Kipf and Max Welling. Variational graph auto-encoders. arXiv preprint arXiv:1611.07308 , 2016b.
• Li et al. (2018) Taisong Li, Jiawei Zhang, S Yu Philip, Yan Zhang, and Yonghong Yan. Deep dynamic network embedding for link prediction. IEEE Access , 6:29219–29230, 2018.
• Loomis (2013) Lynn H Loomis. Introduction to abstract harmonic analysis . Courier Corporation, 2013.
• Ma et al. (2018) Yao Ma, Ziyi Guo, Eric Zhao Zhaochun Ren, and Dawei Yin Jiliang Tang. Streaming graph neural networks. arXiv preprint arXiv:1810.10627 , 2018.
• Monti et al. (2017) Federico Monti, Davide Boscaini, Jonathan Masci, Emanuele Rodola, Jan Svoboda, and Michael M Bronstein. Geometric deep learning on graphs and manifolds using mixture model cnns. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition , pp.  5115–5124, 2017.
• Nguyen et al. (2018) Giang Hoang Nguyen, John Boaz Lee, Ryan A Rossi, Nesreen K Ahmed, Eunyee Koh, and Sungchul Kim. Continuous-time dynamic network embeddings. In Companion Proceedings of the The Web Conference 2018 , pp. 969–976. International World Wide Web Conferences Steering Committee, 2018.
• Pennebaker et al. (2001) James W Pennebaker, Martha E Francis, and Roger J Booth. Linguistic inquiry and word count: Liwc 2001. Mahway: Lawrence Erlbaum Associates , 71(2001):2001, 2001.
• Perozzi et al. (2014) Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining , pp.  701–710. ACM, 2014.
• Rahimi & Recht (2008) Ali Rahimi and Benjamin Recht. Random features for large-scale kernel machines. In Advances in neural information processing systems , pp. 1177–1184, 2008.
• Rahman et al. (2018) Mahmudur Rahman, Tanay Kumar Saha, Mohammad Al Hasan, Kevin S Xu, and Chandan K Reddy. Dylink2vec: Effective feature representation for link prediction in dynamic networks. arXiv preprint arXiv:1804.05755 , 2018.
• Rezende & Mohamed (2015) Danilo Jimenez Rezende and Shakir Mohamed. Variational inference with normalizing flows. arXiv preprint arXiv:1505.05770 , 2015.
• Simonovsky & Komodakis (2017) Martin Simonovsky and Nikos Komodakis. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE conference on computer vision and pattern recognition , pp.  3693–3702, 2017.
• Sukhbaatar et al. (2015) Sainbayar Sukhbaatar, Jason Weston, Rob Fergus, et al. End-to-end memory networks. In Advances in neural information processing systems , pp. 2440–2448, 2015.
• Tang et al. (2015) Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, and Qiaozhu Mei. Line: Large-scale information network embedding. In Proceedings of the 24th international conference on world wide web , pp.  1067–1077. International World Wide Web Conferences Steering Committee, 2015.
• Trivedi et al. (2018) Rakshit Trivedi, Mehrdad Farajtabar, Prasenjeet Biswal, and Hongyuan Zha. Representation learning over dynamic graphs. arXiv preprint arXiv:1803.04051 , 2018.
• Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in neural information processing systems , pp. 5998–6008, 2017.
• Veličković et al. (2017) Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. Graph attention networks. arXiv preprint arXiv:1710.10903 , 2017.
• Wang et al. (2016) Daixin Wang, Peng Cui, and Wenwu Zhu. Structural deep network embedding. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining , pp.  1225–1234. ACM, 2016.
• Wang et al. (2018a) Jizhe Wang, Pipei Huang, Huan Zhao, Zhibo Zhang, Binqiang Zhao, and Dik Lun Lee. Billion-scale commodity embedding for e-commerce recommendation in alibaba. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining , pp.  839–848. ACM, 2018a.
• Wang et al. (2018b) Yue Wang, Yongbin Sun, Ziwei Liu, Sanjay E Sarma, Michael M Bronstein, and Justin M Solomon. Dynamic graph cnn for learning on point clouds. arXiv preprint arXiv:1801.07829 , 2018b.
• Xu et al. (2019a) Da Xu, Chuanwei Ruan, Evren Korpeoglu, Sushant Kumar, and Kannan Achan. Self-attention with functional time representation learning. In Advances in Neural Information Processing Systems , pp. 15889–15899, 2019a.
• Xu et al. (2019b) Da Xu, Chuanwei Ruan, Kamiya Motwani, Evren Korpeoglu, Sushant Kumar, and Kannan Achan. Generative graph convolutional network for growing graphs. In ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) , pp.  3167–3171. IEEE, 2019b.
• Xu et al. (2020) Da Xu, Chuanwei Ruan, Evren Korpeoglu, Sushant Kumar, and Kannan Achan. Product knowledge graph embedding for e-commerce. In Proceedings of the 13th International Conference on Web Search and Data Mining , pp.  672–680, 2020.
• Ying et al. (2018) Rex Ying, Ruining He, Kaifeng Chen, Pong Eksombatchai, William L Hamilton, and Jure Leskovec. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining , pp.  974–983. ACM, 2018.

Appendix A Appendix

A.1 proof for claim 1.

The proof is also shown in our concurrent work Xu et al. ( 2019a ) . We also provide it here for completeness. To prove the results in Claim 1, we alternatively show that under the same condition,

where L Δ = max t ∈ T ~ ⁡ ‖ ∇ Δ ​ ( t ) ‖ subscript 𝐿 Δ subscript 𝑡 ~ 𝑇 norm ∇ Δ 𝑡 L_{\Delta}=\max_{t\in\tilde{T}}\|\nabla\Delta(t)\| (since Δ Δ \Delta is differentiable) with the maximum achieved at t ∗ superscript 𝑡 t^{*} . So we may bound the two events separately.

For | Δ ​ ( t i ) | Δ subscript 𝑡 𝑖 |\Delta(t_{i})| we simply notice that trigeometric functions are bounded between [ − 1 , 1 ] 1 1 [-1,1] , and therefore − 1 ≤ Φ d ℬ ​ ( t 1 ) ′ ​ Φ d ℬ ​ ( t 2 ) ≤ 1 1 subscript superscript Φ ℬ 𝑑 superscript subscript 𝑡 1 ′ subscript superscript Φ ℬ 𝑑 subscript 𝑡 2 1 -1\leq\Phi^{\mathcal{B}}_{d}(t_{1})^{{}^{\prime}}\Phi^{\mathcal{B}}_{d}(t_{2})\leq 1 . The Hoeffding’s inequality for bounded random variables immediately gives us:

So applying the Hoeffding-type union bound to the finite cover gives

For the other event we first apply Markov inequality and obtain:

Also, since E ​ [ s ​ ( t 1 − t 2 ) ] = ψ ​ ( t 1 − t 2 ) 𝐸 delimited-[] 𝑠 subscript 𝑡 1 subscript 𝑡 2 𝜓 subscript 𝑡 1 subscript 𝑡 2 E[s(t_{1}-t_{2})]=\psi(t_{1}-t_{2}) , we have

Combining ( 11 ), ( 12 ) and ( 11 ) gives us:

It is straightforward to examine that the RHS of ( 14 ) is a convex function of N 𝑁 N and is minimized by N ∗ = σ p ​ 2 ​ t max ϵ ​ e ​ x ​ p ​ ( d ​ ϵ 2 32 ) superscript 𝑁 subscript 𝜎 𝑝 2 subscript 𝑡 italic-ϵ 𝑒 𝑥 𝑝 𝑑 superscript italic-ϵ 2 32 N^{*}=\sigma_{p}\sqrt{\frac{2t_{\max}}{\epsilon}}exp(\frac{d\epsilon^{2}}{32}) . Plug N ∗ superscript 𝑁 N^{*} back to ( 14 ) and we obtain ( 9 ). We then solve for d 𝑑 d according to ( 9 ) and obtain the results in Claim 1.

A.2 Comparisons between the attention mechanism of TGAT and GAT

In this part, we provide detailed comparisons between the attention mechanism employed by our proposed TGAT and the GAT proposed by Veličković et al. ( 2017 ) . Other than the obvious fact that GAT does not handle temporal information, the main difference lies in the formulation of attention weights. While GAT depends on the attention mechanism proposed by Bahdanau et al. ( 2014 ) , our architecture refers to the self-attention mechanism of Vaswani et al. ( 2017 ) . Firstly, the attention mechanism used by GAT does not involve the notions of ’query’, ’key’ and ’value’ nor the dot-product formulation introduced in ( 2 ). As a consequence, the attention weight between node v i subscript 𝑣 𝑖 v_{i} and its neighbor v j subscript 𝑣 𝑗 v_{j} is computed via

where 𝐚 𝐚 \mathbf{a} is a weight vector, 𝐖 𝐖 \mathbf{W} is a weight matrix, 𝒩 ​ ( v i ) 𝒩 subscript 𝑣 𝑖 \mathcal{N}(v_{i}) is the neighorhood set for node v i subscript 𝑣 𝑖 v_{i} and 𝐡 i subscript 𝐡 𝑖 \mathbf{h}_{i} is the hidden representation of node v i subscript 𝑣 𝑖 v_{i} . It is then obvious that their computation of α i ​ j subscript 𝛼 𝑖 𝑗 \alpha_{ij} is very different from our approach. In TGAT , after expanding the expressions in Section 3 , the attention weight is computed by:

Intuitively speaking, the attention mechanism of GAT relies on the parameter vector 𝐚 𝐚 \mathbf{a} and the LeakyReLU(.) to capture the hidden factor interactions between entities in the sequence, while we use the linear transformation followed by the dot-product to capture pair-wise interactions of the hidden factors between entities and the time embeddings. The dot-product formulation is important for our approach. From the theoretical perspective, the time encoding functional form is derived according to the notion of temporal kernel 𝒦 𝒦 \mathcal{K} and its inner-product decomposition (Section 3 ). As for the practical performances, we see from Table 1 , 2 and 3 that even after we equip GAT with the same time encoding, the performance is still inferior to our TGAT .

A.3 Details on datasets and preprocessing

Reddit dataset : this benchmark dataset contains users interacting with subreddits by posting under the subreddits. The timestamps tell us when the user makes the posts. The dataset uses the posts made in a one-month span, and selects the most active users and subreddits as nodes, giving a total of 11,000 nodes and around 700,000 temporal edges. The user posts have textual features that are transformed into a 172-dimensional vector representing under the linguistic inquiry and word count (LIWC) categories (Pennebaker et al., 2001 ) . The dynamic binary labels indicate if a user is banned from posting under a subreddit. Since node features are not provided in the original dataset, we use the all-zero vector instead.

Wikipedia dataset : the dataset also collects one-month of interactions induced by users’ editing the Wikipedia pages. The the top edited pages and active users are considered, leading to ∼ similar-to \sim 9,300 nodes and around 160,000 temporal edges. Similar to the Reddit dataset, we also have the ground-truth dynamic labels on whether a user is banned from editing a Wikipedia page. User edits consist of the textual features and are also converted into 172-dimensional LIWC feature vectors. Node features are also not provided, so we also use the all-zero vector as well.

Industrial dataset : we obtain the large-scale customer-product interaction graph from the online grocery shopping platform grocery.walmart.com . We select ∼ similar-to \sim 70,000 most popular products and 100,000 active customers as nodes and use the customer-product purchase interactions over a one-month period as temporal edges ( ∼ similar-to \sim 2 million). Each purchase interaction is timestamped, which we use to construct the temporal graph. The customers are labelled with business tags, indicating if they are interested in dietary products according to their most recent purchase records. Each product node possesses contextual features containing their name, brand, categories and short description. The previous LIWC categories no longer apply since the product contextual features are not natural sentences. We use product embedding approach (Xu et al., 2020 ) to embed each product’s contextual features into a 100-dimensional vector space as preprocessing. The user nodes and edges do not possess features.

We then split the temporal graphs chronologically into 70%-15%-15% for training, validation and testing according to the time epochs of edges, as illustrated in Figure 5 with the Reddit dataset. Since all three datasets have a relatively stationary edge count distribution over time, using the 70 and 85 percentile time points to split the dataset results in approximately 70%-15%-15% of total edges, as suggested by Figure 5 .

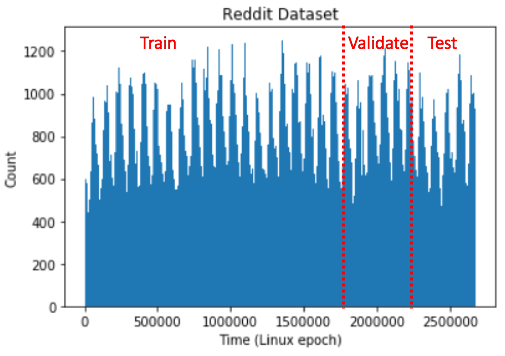
To ensure that an appropriate amount of future edges among the unseen nodes will show up during validation and testing, for each dataset, we randomly sample 10% of nodes, mask them during training and treat them as unseen nodes by only considering their interactions in validation and testing period. This manipulation is necessary since the new nodes that show up during validation and testing period may not have much interaction among themselves. The statistics for the three datasets are summarized in Table 4 .

Preprocessing.

For the Node2vec and DeepWalk baselines who only take static graphs as input, the graph is constructed using all edges in training data regardless of temporal information. For DeepWalk , we treat the recurrent edges as appearing only once, so the graph is unweighted. Although our approach handles both directed and undirected graphs, for the sake of training stability of the baselines, we treat the graphs as undirected . For Node2vec , we use the count of recurrent edges as their weights and construct the weighted graph. For all three datasets, the obtained graphs in both cases are undirected and do not have isolated nodes. Since we choose from active users and popular items, the graphs are all connected .

For the graph convolutional network baselines, i.e. GAE and VGAE , we construct the same undirected weighted graph as for Node2vec . Since GAE and VGAE do not take edge features as input, we use the posts/edits as user node features. For each user in Reddit and Wikipedia dataset, we take the average of their post/edit feature vectors as the node feature. For the industrial dataset where user features are not available, we use the all-zero feature vector instead.

As for the downstream dynamic node classification task, we use the same training, validation and testing dataset as above. Since we aim at predicting the dynamic node labels, for Reddit and Wikipedia dataset we predict if the user node is banned and for the industrial dataset we predict the customers’ business labels, at different time points. Due to the label imbalance, in each of the batch when training for the node label classifier, we conduct stratified sampling such that the label distributions are similar across batches.

A.4 Experiment Setup for Baselines

For all baselines, we set the node embedding dimension to d = 100 𝑑 100 d=100 to keep in accordance with our approach.

Transductive baselines.

Since Node2vec and DeepWalk do not provide room for task-specific manipulation or hacking, we do not modify their default loss function and input format. For both approaches, we select the number of walks among {60,80,100} and the walk-length among {20,30,40} according to the validation AP . Setting number of walks =80 and walk-length =30 give slightly better validation performance compared to others for both approaches. Notice that both Node2vec and DeepWalk use the sigmoid function with embedding inner-products as the decoder to predict neighborhood probabilities. So when predicting whether v i subscript 𝑣 𝑖 v_{i} and v j subscript 𝑣 𝑗 v_{j} will interact in the future, we use σ ​ ( − 𝐳 i ⊺ ​ 𝐳 j ) 𝜎 superscript subscript 𝐳 𝑖 ⊺ subscript 𝐳 𝑗 \sigma(-\mathbf{z}_{i}^{\intercal}\mathbf{z}_{j}) as the score, where 𝐳 i subscript 𝐳 𝑖 \mathbf{z}_{i} and 𝐳 j subscript 𝐳 𝑗 \mathbf{z}_{j} are the node embeddings. Notice that Node2vec has the extra hyper-parameter p 𝑝 p and q 𝑞 q which controls the likelihood of immediately revisiting a node in the walk and interpolation between breadth-first strategy and depth-first strategy. After selecting the optimal number of walks and walk-length under p = 1 𝑝 1 p=1 and q = 1 𝑞 1 q=1 , we further tune the different values of p 𝑝 p in {0.2,0.4,0.6,0.8,1.0} while fixing q = 1 𝑞 1 q=1 . According to validation, p = 0.6 𝑝 0.6 p=0.6 and 0.8 0.8 0.8 give comparable optimal performance.

For the GAE and VGAE baselines, we experiment on using one, two and three graph convolutional layers as the encoder (Kipf & Welling, 2016a ) and use the ReLU ( . ) \text{ReLU}(.) as the activation function. By referencing the official implementation, we also set the dimension of hidden layers to 200. Similar to previous findings, using two layers gives significant performances to using only one layer. Adding the third layer, on the other hand, shows almost identical results for both models. Therefore the results reported are based on two-layer GCN as the encoder. For GAE , we use the standard inner-product decoder as our approach and optimize over the reconstruction loss, and for VGAE , we restrict the Gaussian latent factor space (Kipf & Welling, 2016b ) . Since we have eliminated the temporal information when constructing the input, we find that the optimal hyper-parameters selected according to the tuning have similar patterns as in the previous non-temporal settings.

For the temporal network embedding model CTDNE , the walk length for the temporal random walk is also selected among {60,80,100}, where setting walk length to 80 gives slightly better validation outcome. The original paper considers several temporal edge selection (sampling) methods (uniform, linear and exponential) and finds uniform sampling with best performances (Nguyen et al., 2018 ) . Since our setting is similar to theirs, we adopt the uniform sampling approach.

Inductive baselines.

For the GraphSAGE and GAT baselines, as mentioned before, we train the models in an identical way as our approach with the temporal subgraph batching , despite several slight differences. Firstly, the aggregation layers in GraphSAGE usually considers a fixed neighborhood size via sampling, whereas our approach can take an arbitrary neighborhood as input. Therefore, we only consider the most recent d sample subscript 𝑑 sample d_{\text{sample}} edges during each aggregation for all layers, and we find d sample = 20 subscript 𝑑 sample 20 d_{\text{sample}}=20 gives the best performance among {10,15,20,25}. Secondly, GAT implements a uniform neighborhood dropout. We also experiment with the inverse timespan sampling for neighborhood dropout, and find that it gives slightly better performances but at the cost of computational efficiency, especially for large graphs. We consider aggregating over one, two and three-hop neighborhood for both GAT and GraphSAGE . When working with three hops, we only experiment on GraphSAGE with the mean pooling aggregation. In general, using two hops gives comparable performance to using three hops. Notice that computations with three-hop are costly, since the number of edges during aggregation increase exponentially to the number of hops. Thus we stick to using two hops for GraphSAGE , GAT and our approach. It is worth mentioning that when implementing GraphSAGE -LSTM, the input neighborhood sequences of LSTM are also ordered by their interaction time.

Node classification with baselines.

The dynamic node classification with GraphSAGE and GAT can be conducted similarity to our approach, where we inductively compute the most up-to-date node embeddings and then input them as features to an MLP classifier. For the transductive baselines, it is not reasonable to predict the dynamic node labels with only the fixed node embeddings. Instead, we combine the node embedding with the other node embedding it is interacting with when the label changes, e.g. combine the user embedding with the Wikipedia page embedding that the user attempts on editing when the system bans the user. To combine the pair of node embeddings, we experimented on summation, concatenation and bi-linear transformation. Under summation and concatenation, the combined embeddings are then used as input to an MLP classifier, where the bi-linear transformation directly outputs scores for classification. The validation outcomes suggest that using concatenation with MLP yields the best performance.

A.5 Implementation details

Training. We implement Node2vec using the official C code 5 5 5 https://github.com/snap-stanford/snap/tree/master/examples/node2vec on a 16-core Linux server with 500 Gb memory. DeepWalk is implemented with the official python code 6 6 6 https://github.com/phanein/deepwalk . We refer to the PyTorch geometric library for implementing the GAE and VGAE baselines (Fey & Lenssen, 2019 ) . To accommodate the temporal setting and incorporate edges features, we develop off-the-shelf implementation for GraphSAGE and GAT in PyTorch by referencing their original implementations 7 7 7 https://github.com/williamleif/GraphSAGE 8 8 8 https://github.com/PetarV-/GAT . We also implement our model using PyTorch. All the deep learning models are trained on a machine with one Tesla V100 GPU. We use the Glorot initialization and the Adam SGD optimizer for all models, and apply the early-stopping strategy during training where we terminate the training process if the validation AP score does not improve for 10 epochs.

Downstream node classification. As we discussed before, we use the three-layer MLP as classifier and the (combined) node embeddings as input features from all the experimented approaches, for all three datasets. The MLP is trained with the Glorot initialization and the Adam SGD optimizer in PyTorch as well. The ℓ 2 subscript ℓ 2 \ell_{2} regularization parameter λ 𝜆 \lambda is selected in {0.001, 0.01, 0.05, 0.1, 0.2} case-by-case during training. The early-stopping strategy is also employed.

A.6 Sensitivity analysis and extra ablation study

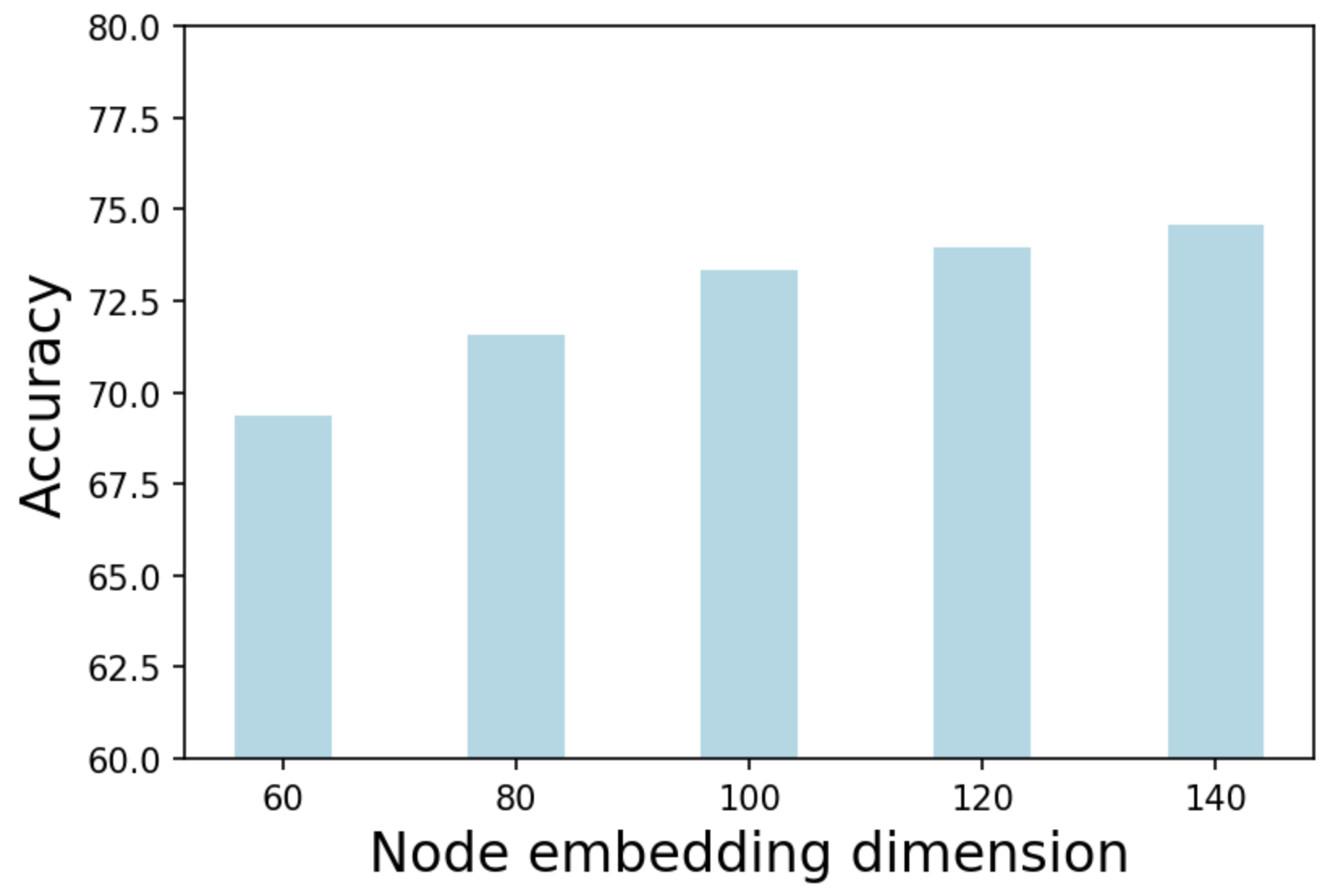
Firstly, we focus on the output node embedding dimension as well as the functional time encoding dimension in this sensitivity analysis. The reported results are averaged over five runs. We experiment on d ∈ { 60 , 80 , 100 , 120 , 140 } 𝑑 60 80 100 120 140 d\in\{60,80,100,120,140\} and d T ∈ { 60 , 80 , 100 , 120 , 140 } subscript 𝑑 𝑇 60 80 100 120 140 d_{T}\in\{60,80,100,120,140\} , and the results are reported in Figure 7(a) and 7(c) . The remaining model setups reported in Section 4.4 are untouched when varying d 𝑑 d or d T subscript 𝑑 𝑇 d_{T} . We observe slightly better outcome when increasing either d 𝑑 d or d T subscript 𝑑 𝑇 d_{T} on the industrial dataset. The patterns on Reddit and Wikipedia dataset are almost identical.

Secondly, we compare between the two methods of learning functional encoding, i.e. using flow-based model or using the non-parametric method introduced in Section 3.1 . We experiment on two flow-based state-of-the-art CDF learning method: normalizing flow (Rezende & Mohamed, 2015 ) and RealNVP (Dinh et al., 2016 ) . We use the default model setups and hyper-parameters in their reference implementations 9 9 9 https://github.com/ex4sperans/variational-inference-with-normalizing-flows 10 10 10 https://github.com/chrischute/real-nvp . We provide the results in Figure 6(b) . As we mentioned before, using flow-based models leads to highly comparable outcomes as the non-parametric approach, but they require longer training time since they implement sampling during each training batch. However, it is possible that carefully-tuned flow-based models can lead to nontrivial improvements, which we leave to the future work.

Finally, we provide sensitivity analysis on the number of attention heads and layers for TGAT . Recall that by stacking two layers in TGAT we are aggregating information from the two-hop neighbourhood. For both accuracy and AP , using three-head attention and two-layers gives the best outcome. In general, the results are relatively stable to the number of heads, and stacking two layers leads to significant improvements compared with using only a single layer.

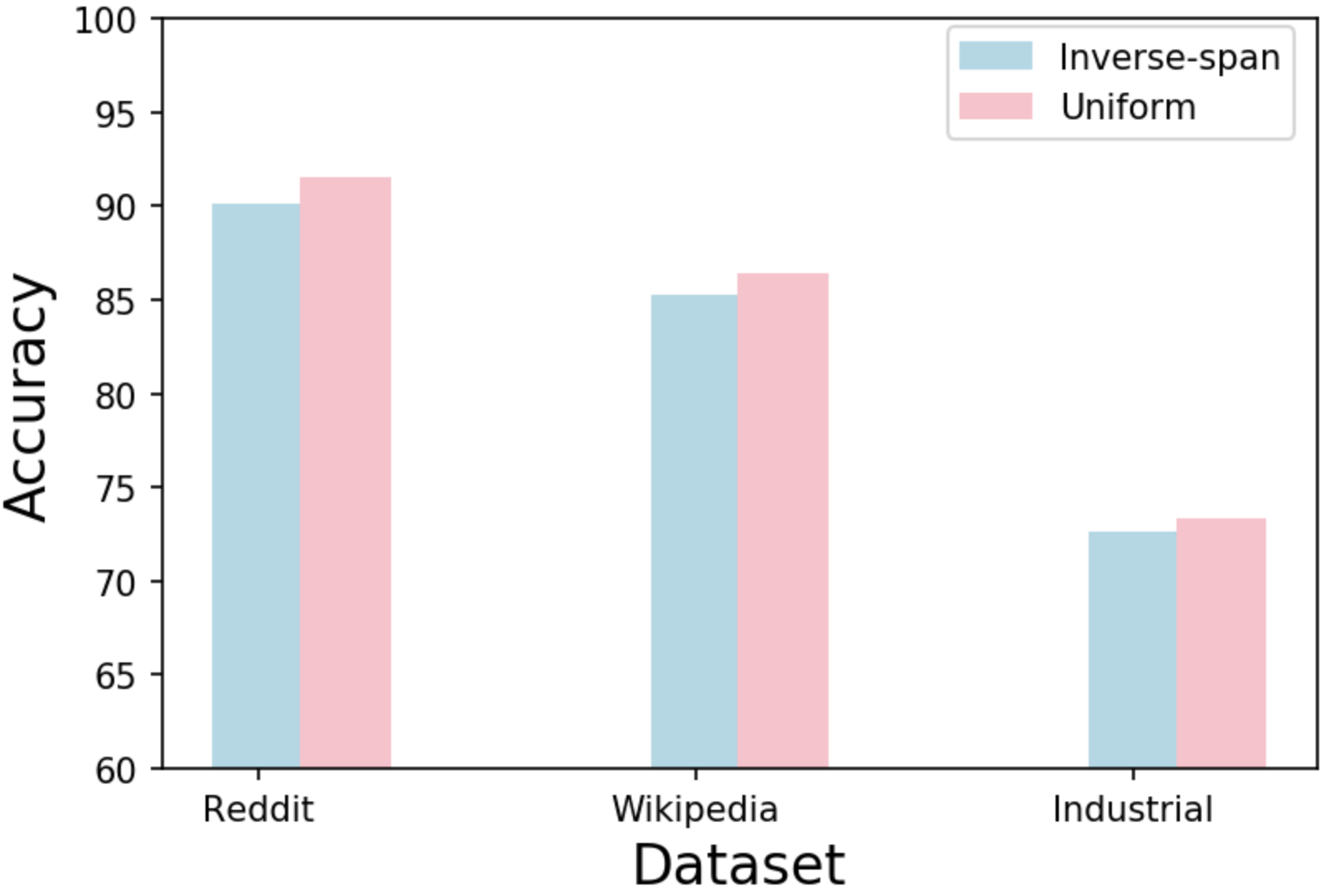
The ablation study for comparing between uniform neighborhood dropout and sampling with inverse timespan is given in Figure 6(a) . The two experiments are carried out under the same setting which we reported in Section 4.4 . We see that using the inverse timespan sampling gives slightly worse performances. This is within expectation since uniform sampling has advantage in capturing the recurrent patterns, which can be important for predicting user actions. On the other hand, the results also suggest the effectiveness of the proposed time encoding for capturing such temporal patterns. Moreover, we point out that using the inverse timespan sampling slows down training, particularly for large graphs where a weighted sampling is conducted within a large number of nodes for each training batch construction. Nonetheless, inverse timespan sampling can help capturing the more recent interactions which may be more useful for certain tasks. Therefore, we suggest to choose the neighborhood dropout method according to the specific use cases.

GTEA: Inductive Representation Learning on Temporal Interaction Graphs via Temporal Edge Aggregation

• Conference paper
• First Online: 28 May 2023
• Cite this conference paper

• Siyue Xie 10 ,
• Yiming Li 10 ,
• Da Sun Handason Tam 10 ,
• Xiaxin Liu 11 ,
• Qiufang Ying 11 ,
• Wing Cheong Lau 10 ,
• Dah Ming Chiu 10 &
• Shouzhi Chen 11  

Part of the book series: Lecture Notes in Computer Science ((LNAI,volume 13936))

Included in the following conference series:

• Pacific-Asia Conference on Knowledge Discovery and Data Mining

1248 Accesses

1 Citations

In this paper, we propose the Graph Temporal Edge Aggregation (GTEA) framework for inductive learning on Temporal Interaction Graphs (TIGs). Different from previous works, GTEA models the temporal dynamics of interaction sequences in the continuous-time space and simultaneously takes advantage of both rich node and edge/ interaction attributes in the graph. Concretely, we integrate a sequence model with a time encoder to learn pairwise interactional dynamics between two adjacent nodes. This helps capture complex temporal interactional patterns of a node pair along the history, which generates edge embeddings that can be fed into a GNN backbone. By aggregating features of neighboring nodes and the corresponding edge embeddings, GTEA jointly learns both topological and temporal dependencies of a TIG. In addition, a sparsity-inducing self-attention scheme is incorporated for neighbor aggregation, which highlights more important neighbors and suppresses trivial noises for GTEA. By jointly optimizing the sequence model and the GNN backbone, GTEA learns more comprehensive node representations capturing both temporal and graph structural characteristics. Extensive experiments on five large-scale real-world datasets demonstrate the superiority of GTEA over other inductive models.

S. Xie and Y. Li—Equal contributions.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Dynamic Recurrent Embedding for Temporal Interaction Networks

Transformer-Based Representation Learning on Temporal Heterogeneous Graphs

DynGraphGAN: Dynamic Graph Embedding via Generative Adversarial Networks

Appendix can be found in: https://github.com/xslangley/GTEA .

Raw data: https://www.kaggle.com/xblock/ethereum-phishing-transaction-network .

Bielak, P., Kajdanowicz, T., Chawla, N.V.: Attre2vec: unsupervised attributed edge representation learning. arXiv preprint arXiv:2012.14727 (2020)

Gong, L., Cheng, Q.: Exploiting edge features for graph neural networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 9211–9219 (2019)

Google Scholar  

Grover, A., Leskovec, J.: node2vec: Scalable feature learning for networks. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 855–864 (2016)

Hamilton, W., Ying, Z., Leskovec, J.: Inductive representation learning on large graphs. In: Advances in Neural Information Processing Systems, pp. 1024–1034 (2017)

Hochreiter, S., Schmidhuber, J.: Long short-term memory. Neural Comput. 9 (8), 1735–1780 (1997)

Article   Google Scholar  

Huang, S., Bao, Z., Culpepper, J.S., Zhang, B.: Finding temporal influential users over evolving social networks. In: 2019 IEEE 35th International Conference on Data Engineering (ICDE), pp. 398–409. IEEE (2019)

Jiang, X., Zhu, R., Li, S., Ji, P.: Co-embedding of nodes and edges with graph neural networks. IEEE Trans. Pattern Anal. Mach. Intell. (2020)

Kipf, T.N., Welling, M.: Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907 (2016)

Kumar, S., Zhang, X., Leskovec, J.: Predicting dynamic embedding trajectory in temporal interaction networks. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1269–1278 (2019)

Li, Y., Yu, R., Shahabi, C., Liu, Y.: Diffusion convolutional recurrent neural network: data-driven traffic forecasting. In: International Conference on Learning Representations (ICLR) (2018)

Ma, Y., Guo, Z., Ren, Z., Tang, J., Yin, D.: Streaming graph neural networks. In: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, pp. 719–728 (2020)

Martins, A., Astudillo, R.: From softmax to sparsemax: a sparse model of attention and multi-label classification. In: International Conference on Machine Learning, pp. 1614–1623 (2016)

Mehran Kazemi, S., et al.: Time2vec: learning a vector representation of time. arXiv preprint arXiv:1907.05321 (2019)

Nguyen, G.H., Lee, J.B., Rossi, R.A., Ahmed, N.K., Koh, E., Kim, S.: Continuous-time dynamic network embeddings. In: Companion Proceedings of the Web Conference 2018, pp. 969–976 (2018)

Qiu, Z., Hu, W., Wu, J., Liu, W., Du, B., Jia, X.: Temporal network embedding with high-order nonlinear information. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol. 34, pp. 5436–5443 (2020)

Qu, L., Zhu, H., Duan, Q., Shi, Y.: Continuous-time link prediction via temporal dependent graph neural network. In: Proceedings of the Web Conference 2020, pp. 3026–3032 (2020)

Rahimi, A., Recht, B.: Random features for large-scale kernel machines. In: Advances in Neural Information Processing Systems, pp. 1177–1184 (2008)

Rossi, E., Chamberlain, B., Frasca, F., Eynard, D., Monti, F., Bronstein, M.: Temporal graph networks for deep learning on dynamic graphs. arXiv preprint arXiv:2006.10637 (2020)

Shi, Y., Huang, Z., Wang, W., Zhong, H., Feng, S., Sun, Y.: Masked label prediction: unified message passing model for semi-supervised classification. arXiv preprint arXiv:2009.03509 (2020)

Simonovsky, M., Komodakis, N.: Dynamic edge-conditioned filters in convolutional neural networks on graphs. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3693–3702 (2017)

Singer, U., Guy, I., Radinsky, K.: Node embedding over temporal graphs. In: Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19, pp. 4605–4612. International Joint Conferences on Artificial Intelligence Organization, July 2019. https://doi.org/10.24963/ijcai.2019/640

Trivedi, R., Dai, H., Wang, Y., Song, L.: Know-evolve: Deep temporal reasoning for dynamic knowledge graphs. arXiv preprint arXiv:1705.05742 (2017)

Trivedi, R., Farajtabar, M., Biswal, P., Zha, H.: Dyrep: learning representations over dynamic graphs (2018)

Vaswani, A., et al.: Attention is all you need. In: Advances in Neural Information Processing Systems, pp. 5998–6008 (2017)

Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., Bengio, Y.: Graph attention networks. arXiv preprint arXiv:1710.10903 (2017)

Wang, Y., Sun, Y., Liu, Z., Sarma, S.E., Bronstein, M.M., Solomon, J.M.: Dynamic graph CNN for learning on point clouds. ACM Trans. Graph. (TOG) 38 (5), 1–12 (2019)

Xu, D., Ruan, C., Korpeoglu, E., Kumar, S., Achan, K.: Inductive representation learning on temporal graphs. arXiv preprint arXiv:2002.07962 (2020)

Yu, B., Yin, H., Zhu, Z.: Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting. In: Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI) (2018)

Zhang, J., Shi, X., Xie, J., Ma, H., King, I., Yeung, D.Y.: GAAN: gated attention networks for learning on large and spatiotemporal graphs. arXiv preprint arXiv:1803.07294 (2018)

Zhang, Z., et al.: Learning temporal interaction graph embedding via coupled memory networks. In: Proceedings of The Web Conference 2020, pp. 3049–3055 (2020)

Zuo, Y., Liu, G., Lin, H., Guo, J., Hu, X., Wu, J.: Embedding temporal network via neighborhood formation. In: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 2857–2866 (2018)

Download references

Acknowledgements

This research is supported in part by the Innovation and Technology Committee of HKSAR under the project#ITS/244/16, the CUHK MobiTeC R &D Fund and a gift from Tencent.

Author information

Authors and affiliations.

The Chinese University of Hong Kong, Hong Kong, China

Siyue Xie, Yiming Li, Da Sun Handason Tam, Wing Cheong Lau & Dah Ming Chiu

Tencent Technology Co. Ltd., Shenzhen, China

Xiaxin Liu, Qiufang Ying & Shouzhi Chen

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Siyue Xie .

Editor information

Editors and affiliations.

Kyoto University, Kyoto, Japan

Hisashi Kashima

IBM Research, Thomas J. Watson Research Center, Yorktown Heights, NY, USA

Tsuyoshi Ide

National Chiao Tung University, Hsinchu, Taiwan

Wen-Chih Peng

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Cite this paper.

Xie, S. et al. (2023). GTEA: Inductive Representation Learning on Temporal Interaction Graphs via Temporal Edge Aggregation. In: Kashima, H., Ide, T., Peng, WC. (eds) Advances in Knowledge Discovery and Data Mining. PAKDD 2023. Lecture Notes in Computer Science(), vol 13936. Springer, Cham. https://doi.org/10.1007/978-3-031-33377-4_3

Download citation

DOI : https://doi.org/10.1007/978-3-031-33377-4_3

Published : 28 May 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-33376-7

Online ISBN : 978-3-031-33377-4

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research