laplace experiment mathematik

Teste dein Wissen zum Thema Laplace Experiment!

Laplace experiment.

In diesem Artikel dreht sich alles um Laplace . Von der Laplace Wahrscheinlichkeit bis hin zum Laplace Würfel wird dir alles zu Laplace Experimenten erklärt.

Du möchtest wissen:  Was ist ein Laplace Experiment ? In unsrem Video erfährst du bequem und einfach was genau es bedeutet, wenn einem Zufallsexperiment die Laplace Bedingung zugrunde liegt.

Laplace Experiment Definition

Laplace wahrscheinlichkeit, laplace experiment aufgaben, laplace experiment — häufigste fragen, wahrscheinlichkeitsrechnung.

Ein Laplace Experiment ist ein Zufallsexperiment, bei dem alle elementaren Ergebnisse die selbe Wahrscheinlichkeit haben. Die dazugehörige Laplace Wahrscheinlichkeit wird mit der Laplace Formel berechnet, welche sich durch die Division der Anzahl des Ereignisses durch alle möglichen Ergebnisse ergibt.

Laplace Experiment Erklärung

Generell unterscheidet man in der Statistik unterscheidet verschiedene Spezialfälle von Wahrscheinlichkeiten. Einer dieser Sonderfälle ist die Laplace Wahrscheinlichkeit . Diese liegt den dazugehörigen Laplace Experimenten zugrunde und setzt voraus, dass alle elementaren Ergebnisse des Zufallsexperimentes die gleiche Wahrscheinlichkeit haben. Einfach gesagt, muss jedes mögliches Szenario gleich wahrscheinlich sein, damit von Laplace die Rede sein kann.

Laplace Experiment Beispiele

Das gängigste Beispiel für einen Laplace Versuch ist das Werfen eines ungezinkten Würfels. Ungezinkt bedeutet, dass dieser nicht manipuliert ist und, dass alle sechs Seiten mit gleicher Wahrscheinlichkeit gewürfelt werden. Bei einem Laplace Würfel fällt die 1 also genau gleich oft wie die 6, wenn man unendlich oft würfeln würde. Weitere Beispiele sind das Werfen einer Münze oder das drehen an einem Glücksrad. Die Wahrscheinlichkeit Kopf oder Zahl zu werfen beträgt dann nämlich jeweils genau 50%. Bei dem letzteren Beispiel muss zusätzlich beachten werden, dass alle möglichen Felder gleich häufig vorkommen müssen, damit die Laplace Bedingung erfüllt ist.

Du weist jetzt, dass jedem Laplace Experiment die Laplace Wahrscheinlichkeit zugrunde liegt. Die Bedingung, dass alle Versuchsausgänge gleich wahrscheinlich sind muss also erfüllt sein. Aber woher weiß man, ob diese Grundbedingung gegeben ist oder nicht?

Kein Laplace Experiment?

Wenn du also die Wahrscheinlichkeit für ein Ereignis bestimmen sollst, prüfe zunächst ob es sich bei dem Zufallsexperiment überhaupt um einen Laplace Versuch handelt oder nicht. Hier spricht man auch vom sogenannten Elementarereignis ω , also einem Ereignis, für das die Eintrittswahrscheinlichkeit immer gleich hoch ist. Es gilt:

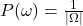
Laplace Formel

Allgemein ist die Wahrscheinlichkeit in einem Laplace Experiment für ein Ereignis A durch die Laplace Formel wie folgt definiert:

Abschließend schauen wir uns noch zwei praktische Beispiele von Laplace Experimenten an. So wird deutlich wie man die Wahrscheinlichkeit dieser Zufallsexperimente einfach mit der Laplace Formel berechnen kann.

Laplace Würfel

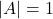
Laplace Experiment Beispiel: Roulette

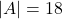
Die Wahrscheinlichkeit eine rote Zahl zu würfeln liegt also bei ungefähr 49%.

Das war auch schon alles Wichtige ! Zur Wiederholung hier nochmal die zentrale Formel:

• Was ist ein Laplace Experiment? Ein Laplace Experiment ist ein Zufallsexperiment, bei dem alle Ergebnisse dieselbe Wahrscheinlichkeit haben, einzutreffen. Ein typisches Beispiel hierfür ist der Wurf eines Würfels. Jede Augenzahl hat dieselbe Wahrscheinlichkeit gewürfelt zu werden, nämlich 1/6.   
• Was ist die Laplace Formel? Die Laplace Formel bestimmt die Wahrscheinlichkeit eines Ereignisses (E) im Laplace Experiment. Wenn die Gesamtzahl aller möglichen Ergebnisse n ist, berechnet sich die Wahrscheinlichkeit mit P(E) = 1/n.  
• Wie läuft ein Laplace Versuch ab? In einem Laplace Versuch (Experiment) müssen alle möglichen Ereignisse mit gleicher Wahrscheinlichkeit stattfinden. Das heißt, dass jedes zufällige Ergebnis gleich hohe Chancen hat, einzutreffen. Ein typisches Beispiel für ein Laplace Versuch ist der Wurf eines fairen Würfels.

Neben dem Laplace Experiment gibt es noch andere Zufallsexperimente. Wie du dann die Wahrscheinlichkeit berechnest , erfährst du hier!

Beliebte Inhalte aus dem Bereich Wahrscheinlichkeitsrechnung

• Bedingte Wahrscheinlichkeit Dauer: 02:16
• Vierfeldertafel Dauer: 04:46
• Satz der totalen Wahrscheinlichkeit Dauer: 01:58

Weitere Inhalte: Wahrscheinlichkeitsrechnung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke! Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung . Bitte lade anschließend die Seite neu .

Lerninhalte finden

• Abituraufgaben
• Französisch
• Psychologie
• Germanistik
• Ingenieurwissenschaften
• Rechtswissenschaften
• Umweltwissenschaft
• Gastronomie und Tourismus
• Kaufmännische
• Zahnmedizinische Fachangestellte
• Laplace Experiment

In der Welt der Mathematik ist das Laplace-Experiment ein zentraler Aspekt der Wahrscheinlichkeitsrechnung . Die Einführung in das Laplace Experiment bietet eine detaillierte Erklärung für das Verständnis von Ereignissen und Wahrscheinlichkeiten. Hier erhältst du eine präzise Definition, die Unterschiede zwischen Laplace und Nicht-Laplace Experimenten sowie konkrete Beispiele. Weiterführend gibt es Informationen zur Berechnung von Ereignissen im Laplace Experiment, die Anwendung der Formel und wie man ein solches Experiment mit Hilfe von Baumdiagrammen darstellt. Schließlich werden alle Merkmale eines Laplace Experiments im Überblick dargestellt. Ein wissensreicher und informativer Start in die Welt der empirischen Wahrscheinlichkeit .

Lerne mit Millionen geteilten Karteikarten

• Cell Biology

Was würde die Wahrscheinlichkeit für die Aufgabe, eine gerade Zahl oder eine 5 bei einem Würfelwurf zu bekommen, sein?

Was ist ein Baumdiagramm in Bezug auf ein Laplace Experiment?

Wie erstellt man ein Baumdiagramm für ein Laplace Experiment?

Was ist ein Laplace Experiment?

Wie berechnest du die Wahrscheinlichkeit eines spezifischen Ereignisses in einem Laplace-Experiment?

Was steht "P(E)" in der Formel P(E) = 1/n für?

Wie berechnet man die Wahrscheinlichkeit eines Ereignisses in einem Laplace Experiment?

Wie viele Endpunkte hat ein Baumdiagramm im Fall von zwei Würfen zweier Würfel?

Nenne ein Beispiel für ein Laplace Experiment und ein Nicht-Laplace Experiment.

Wie berechnest du die Wahrscheinlichkeit für ein Ereignis, bei dem mehrere Ergebnisse gültig sind, in einem Laplace-Experiment?

Was sind die Merkmale eines Laplace Experiments?

Schreib bessere Noten mit StudySmarter Premium

Geld-zurück-Garantie, wenn du durch die Prüfung fällst

Review generated flashcards

um mit dem Lernen zu beginnen oder eigene AI-Karteikarten zu erstellen

Erstelle unlimitiert Karteikarten auf StudySmarter

StudySmarter Redaktionsteam

Team Laplace Experiment Lehrer

• 10 Minuten Lesezeit
• Geprüft vom StudySmarter Redaktionsteam
• Berühmte Mathematiker
• 3M Aufgaben
• Absolute Häufigkeit
• Additionssatz
• Allgemeine Zählprinzipien
• Axiome von Kolmogorow
• Balkendiagramm
• Baumdiagramm
• Bedingte Wahrscheinlichkeit
• Bernoulli Experiment
• Bernoulli Formel
• Bernoulli Verteilung
• Binomialkoeffizient
• Binomialkoeffizient Kombinatorik
• Binomialverteilung
• De Morgansche Regeln
• Deskriptive Statistik
• Diagramm auswerten
• Diskrete Verteilung
• Einseitiger Hypothesentest
• Erwartungswert
• Exponentialverteilung
• Fehler Hypothesentest
• Gauß-Verteilung
• Gesetz der großen Zahlen
• Gleichverteilung
• Grundgesamtheit Stichprobe
• Hypergeometrische Verteilung
• Hypothesentest
• Inferenzstatistik
• Irrtumswahrscheinlichkeit
• Kombination mit Wiederholung
• Kombination ohne Wiederholung
• Kombinationen
• Kombinatorik
• Konfidenzintervall
• Kreisdiagramm
• Kugel Fächer Modell
• Kumulierte Binomialverteilung
• Lotto Formel
• Mehrstufige Zufallsexperimente
• Mengenalgebra
• Multiplikationssatz
• Normalverteilung
• Nullhypothese
• Näherungsformel
• Permutation
• Permutation mit Wiederholung
• Permutation ohne Wiederholung
• Pfadmultiplikationsregel
• Poisson Verteilung
• Produktregel Kombinatorik
• Regeln Wahrscheinlichkeitsrechnung
• Relative Häufigkeit
• Satz von Bayes
• Sigma Regeln
• Signifikanzniveau
• Simulation Wahrscheinlichkeit
• Simulation von Zufallsexperimenten
• Skalenniveau
• Standardabweichung berechnen
• Stetige Verteilung
• Stochastische Unabhängigkeit
• Streudiagramm
• Streuungsmaß
• Summenregel Wahrscheinlichkeit
• Säulendiagramm
• Taxi Problem
• Totale Wahrscheinlichkeit
• Unabhängige Zufallsvariablen
• Variation mit Wiederholung
• Variation ohne Wiederholung
• Venn-Diagramm
• Verteilungsfunktion
• Vierfeldertafel
• Wahrscheinlichkeit
• Wahrscheinlichkeitsfunktion
• Wahrscheinlichkeitsraum
• Wahrscheinlichkeitsrechnung
• Wahrscheinlichkeitsverteilung
• Ziegenproblem
• Zufallsexperiment
• Zufallsgrößen und Wahrscheinlichkeitsverteilung
• Zweiseitiger Hypothesentest

Springe zu einem wichtigen Kapitel

Einführung in das Laplace Experiment

Was ist ein laplace experiment: definition.

Ein Laplace Experiment ist ein zufälliges Experiment, bei dem alle möglichen Ausgänge gleich wahrscheinlich sind. Das bedeutet, dass jedes Ereignis die gleiche Chance hat, ein Ergebnis des Experiments zu sein. Ein klassisches Beispiel für ein Laplace Experiment ist der Wurf eines fairen Würfels. Jeder der sechs möglichen Ausgänge (1, 2, 3, 4, 5, 6) hat die gleiche Wahrscheinlichkeit .

Wenn du beispielsweise einen fairen Würfel wirfst, beträgt die Wahrscheinlichkeit, eine "6" zu würfeln, \( P(E) = \frac{1}{6} \), da es sechs mögliche Ergebnisse gibt, und jedes Ergebnis ist gleich wahrscheinlich.

Unterschied zwischen Laplace und Nicht-Laplace Experiment

Ein Nicht-Laplace Experiment ist ein zufälliges Experiment, bei dem die Wahrscheinlichkeiten der verschiedenen möglichen Ereignisse nicht gleich sind. Hier variiert die Wahrscheinlichkeit der verschiedenen möglichen Ergebnisse.

Beispiele für Laplace Experimente und Nicht-Laplace Experimente

Nehmen wir das Beispiel der Auswahl einer Person aus einer Gruppe. Hierbei spricht man von einem Nicht-Laplace Experiment, weil das Geschlecht, das Alter oder andere Faktoren die Auswahl beeinflussen können und daher nicht alle Personen die gleiche Auswahlwahrscheinlichkeit haben.

Das Verständnis des Unterschieds zwischen Laplace und Nicht-Laplace Experimenten ist essenziell, wenn du dich mit Wahrscheinlichkeiten beschäftigst. Es hilft dabei, realistische Annahmen zu treffen und statistische Modelle auf reale Situationen anzuwenden.

Berechnung des Laplace Experiments

Anwendung der formel im laplace experiment.

Die Formel bedeutet also: Die Wahrscheinlichkeit eines Ereignisses in einem Laplace Experiment ist gleich dem Kehrwert der Anzahl aller möglichen Ergebnisse.

Wenn du beispielsweise eine Spielkarte aus einem gemischten Kartenspiel mit 52 Karten ziehst, beträgt die Wahrscheinlichkeit, dass es sich um einen König handelt, \( P(E) = \frac{1}{13} \). Denn das Deck hat vier Könige und 52 mögliche Karten, die gezogen werden können.

Praktische Laplace Experiment Aufgaben und Lösungen

• Für Aufgabe 1: Ein Kartenspiel enthält 52 Karten, von denen 13 Herzkarten sind. Also beträgt die Wahrscheinlichkeit, dass eine Ziehung ein Herz ist, \( P(E) = \frac{13}{52} = \frac{1}{4} \).
• Für Aufgabe 2: Ein Würfel hat sechs Seiten, und zwei davon sind 2 und 4. Also beträgt die Wahrscheinlichkeit, eine 2 oder 4 zu würfeln, \( P(E) = \frac{2}{6} = \frac{1}{3} \).

Theorie und Praxis gehen Hand in Hand. Indem du Beispielaufgaben löst, vertiefst du dein Verständnis für die Berechnung der Wahrscheinlichkeit in einem Laplace Experiment.

Berechnung von Ereignissen im Laplace Experiment

Wenn mehrere Ergebnisse für ein Ereignis gültig sind, addiere die Wahrscheinlichkeiten dieser Ergebnisse. Zum Beispiel: Die Wahrscheinlichkeit, eine gerade Zahl beim Würfeln zu bekommen, ist die Summe der Wahrscheinlichkeiten, eine 2, 4 oder 6 zu würfeln.

Für eine Aufgabe, in der wir die Wahrscheinlichkeit berechnen sollen, eine gerade Zahl oder eine 5 zu würfeln, addieren wir die Wahrscheinlichkeiten des Ereignisses "gerade Zahl würfeln" und des Ereignisses "5 würfeln". Diese Berechnung würde folgendermaßen aussehen: \( P(E) = P(\text{2 oder 4 oder 6}) + P(\text{5}) = \frac{3}{6} + \frac{1}{6} = \frac{4}{6} = \frac{2}{3} \).

Darstellung des Laplace Experiments

Einsatz des baumdiagramms im laplace experiment.

Ein Baumdiagramm ist ein grafisches Werkzeug, das verwendet wird, um alle möglichen Ergebnisse eines Experiments zu zeigen. Dabei repräsentiert jeder Ast des Baums eine mögliche Entscheidung oder ein mögliches Ergebnis.

Angenommen, du würdest eine faire Münze zweimal hintereinander werfen. Du würdest mit einem Ausgangspunkt beginnen und von dort aus zwei Linien zeichnen, eine für "Kopf" und eine für "Zahl". Von jedem dieser Punkte aus würdest du erneut zwei Linien zeichnen, wieder jeweils eine für "Kopf" und "Zahl". So endest du mit vier Endpunkten, die für die vier möglichen Ergebnisse des Experiments stehen: Kopf-Kopf, Kopf-Zahl, Zahl-Kopf und Zahl-Zahl. An jeder Linie würde dann noch die jeweilige Wahrscheinlichkeit stehen, also im Falle unserer fairen Münze immer \( \frac{1}{2} \) für jeden Zweig.

Laplace Experiment Beispiele mit Baumdiagrammen

Die Anzahl der Endpunkte in einem Baumdiagramm für ein Laplace Experiment entspricht der Anzahl der möglichen Ausgänge des Experiments. Sie gibt also die Anzahl der Ereignisse im Ereignisraum an.

Merkmale eines Laplace Experiments: Ein Überblick

Wenn du eine faire Münze wirfst, sind diese Eigenschaften alle sichtbar. Die zwei möglichen Ergebnisse (Kopf oder Zahl) sind gleich wahrscheinlich, deine Wahl ist zufällig und unabhängig von vorherigen oder nachfolgenden Würfen und es gibt eine begrenzte Anzahl an möglichen Ausgängen (nämlich zwei).

Ein tieferes Verständnis der Merkmale eines Laplace Experiments hilft dir, die Konzepte der Wahrscheinlichkeitsrechnung besser zu begreifen und korrekt anzuwenden.

Laplace Experiment - Das Wichtigste

• Laplace Experiment: zufälliges Experiment, bei dem alle möglichen Ausgänge gleich wahrscheinlich sind
• Formel zur Berechnung der Wahrscheinlichkeit eines Ereignisses in einem Laplace Experiment: P(E) = 1/n
• Unterschied Laplace zu Nicht-Laplace Experiment: Bei einem Nicht-Laplace Experiment sind nicht alle Ergebnisse gleich wahrscheinlich
• Beispiele: Wurf eines fairen Würfels (Laplace), Wurf eines gezinkten Würfels (Nicht-Laplace)
• Berechnung von Ereignissen: Bei mehreren gültigen Ergebnissen die Wahrscheinlichkeiten dieser addieren
• Baumdiagramm: Visualisierung aller potenziellen Ergebnisse und ihrer Wahrscheinlichkeiten
• Merkmale eines Laplace Experiments: Gleichwahrscheinlichkeit, Zufälligkeit, Unabhängigkeit, begrenzte Anzahl an Ausgängen

Karteikarten in Laplace Experiment 12

Die Wahrscheinlichkeit beträgt 2/3, weil du die Wahrscheinlichkeiten der Ereignisse "gerade Zahl würfeln" und "5 würfeln" addierst.

Ein Baumdiagramm ist ein Diagramm, das den Verlauf von Experimenten zeigt, bei denen mehrere Ereignisse aufeinanderfolgen oder gleichzeitig auftreten können. Jeder Zweig des Diagramms entspricht einem möglichen Ergebnis. Dies erlaubt es, eine klare visuelle Darstellung aller potenziellen Ergebnisse und ihrer jeweiligen Wahrscheinlichkeiten zu liefern.

Man beginnt mit einem Ausgangspunkt, von dem aus so viele Linien (Zweige) erstellt werden, wie es mögliche erste Ergebnisse gibt. Für jedes Ergebnis zieht man weitere Linien für die nächsten möglichen Ergebnisse. Dies wiederholt man, bis alle Ergebnisse dargestellt sind.

Ein Laplace Experiment ist ein zufälliges Experiment, bei dem alle möglichen Ausgänge gleich wahrscheinlich sind, wie beispielsweise beim Wurf eines fairen Würfels.

Du verwendest die Formel P(E) = 1/n, wobei "n" die Gesamtzahl der möglichen Ergebnisse ist.

"P(E)" repräsentiert die Wahrscheinlichkeit des auftretenden Ereignisses "E".

Lerne schneller mit den 12 Karteikarten zu Laplace Experiment

Melde dich kostenlos an, um Zugriff auf all unsere Karteikarten zu erhalten.

Du hast bereits ein Konto? Anmelden

Häufig gestellte Fragen zum Thema Laplace Experiment

Teste dein wissen mit multiple-choice-karteikarten, das war ein fantastischer start, das kannst du besser, melde dich an, um deine eigenen karteikarten zu erstellen.

Greife auf über 700 Millionen Lernmaterialien zu

Lerne effizienter mit Karteikarten

Erziele bessere Noten mit AI

Hast du bereits ein Konto? Logge dich ein  

Bleib am Ball, du machst das großartig.

Entdecke Lernmaterialien mit der kostenlosen StudySmarter App

Über StudySmarter

StudySmarter ist ein weltweit anerkanntes Bildungstechnologie-Unternehmen, das eine ganzheitliche Lernplattform für Schüler und Studenten aller Altersstufen und Bildungsniveaus bietet. Unsere Plattform unterstützt das Lernen in einer breiten Palette von Fächern, einschließlich MINT, Sozialwissenschaften und Sprachen, und hilft den Schülern auch, weltweit verschiedene Tests und Prüfungen wie GCSE, A Level, SAT, ACT, Abitur und mehr erfolgreich zu meistern. Wir bieten eine umfangreiche Bibliothek von Lernmaterialien, einschließlich interaktiver Karteikarten, umfassender Lehrbuchlösungen und detaillierter Erklärungen. Die fortschrittliche Technologie und Werkzeuge, die wir zur Verfügung stellen, helfen Schülern, ihre eigenen Lernmaterialien zu erstellen. Die Inhalte von StudySmarter sind nicht nur von Experten geprüft, sondern werden auch regelmäßig aktualisiert, um Genauigkeit und Relevanz zu gewährleisten.

Team Mathe Lehrer

Lerne jederzeit. Lerne überall. Auf allen Geräten.

Erstelle ein kostenloses konto, um diese erklärung zu speichern..

Speichere Erklärungen in deinem persönlichen Bereich und greife jederzeit und überall auf sie zu!

Durch deine Registrierung stimmst du den AGBs und der Datenschutzerklärung von StudySmarter zu.

Du hast schon einen Account? Anmelden

Melde dich an für Notizen & Bearbeitung. 100% for free.

Schließ dich über 22 Millionen Schülern und Studierenden an und lerne mit unserer StudySmarter App!

Die erste Lern-App, die wirklich alles bietet, was du brauchst, um deine Prüfungen an einem Ort zu meistern.

• Karteikarten & Quizze
• KI-Lernassistent
• Probeklausuren
• Intelligente Notizen

Laplace Experiment: Regel, Beispiele, Aufgaben

Laplace experiment - definition, beispiele für laplace experimente, was sind keine laplace-aufgaben.

In diesem Lerntext erklären wir dir alles zum Thema Laplace-Experimente , eine Art von Zufallsexperimenten, die du aus deinem Mathematikunterricht schon kennen wirst. Du wirst schnell verstehen, wie du bei dieser Art von Zufallsversuchen rechnest. Am Ende kannst du dein erlerntes Wissen zu Laplace und Wahrscheinlichkeiten in Aufgaben weiter vertiefen und kontrollieren.

Ein Laplace Experiment ist eigentlich nichts anderes als das, was du in deinem Matheunterricht als Zufallsversuch kennenlernst - mit einer kleinen Einschränkung: Ein Laplace Experiment ist ein Zufallsversuch, bei dem die Wahrscheinlichkeiten aller möglichen Ergebnisse gleich sind . Typische Beispiele bei Laplace sind in der Regel das Werfen einer Münze oder eines gewöhnlichen Würfels. Das Besondere an diesen Versuchen ist, dass sie uns das Rechnen mit Wahrscheinlichkeiten vereinfachen. In Laplace-Experimenten gilt die Regel:

$P (E) = \frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ der\ möglichen\ Ergebnisse}$

Wir müssen also einfach die Anzahl der Ergebnisse, die gewünscht sind, durch die Anzahl aller Ergebnisse dividieren.

Ein Laplace Experiment ist ein Zufallsversuch, bei dem die Wahrscheinlichkeiten aller möglichen Ergebnisse gleich sind.

Wie du siehst, ist die Rechnung für dich nicht neu. Und das ist nicht verwunderlich, da die allermeisten Zufallsexperimente, die du bis jetzt kennengelernt hast, Laplace-Experimente sind. Im Lerntext Zufallsversuche - Wahrscheinlichkeit von Ergebnissen berechnen kannst du nochmal alles Weitere dazu nachlesen.

Gut zu wissen

Pierre-Simon Laplace war ein französischer Mathematiker und Physiker, der um 1800 zu den Themen Wahrscheinlichkeitsrechnung und Differentialgleichungen forschte. Der Name Laplace kann dir in deinem Mathematikunterricht noch öfter begegnen.

Betrachten wir nun einige Beispiele, um den Unterschied zwischen Laplace-Experimenten und anderen Zufallsversuchen zu verstehen.

• Über 700 Lerntexte & Videos
• Über 250.000 Übungen & Lösungen
• Sofort-Hilfe: Lehrer online fragen
• Gratis Nachhilfe-Probestunde

Das erste "Laplace-Beispiel" ist ein wirklicher Klassiker in der Wahrscheinlichkeitsrechnung: das einmalige Werfen eines Würfels. Ein normaler Würfel hat sechs Seiten, die mit den Zahlen 1 bis 6 beschriftet sind. Jede Zahl hat die gleiche Wahrscheinlichkeit, gewürfelt zu werden.

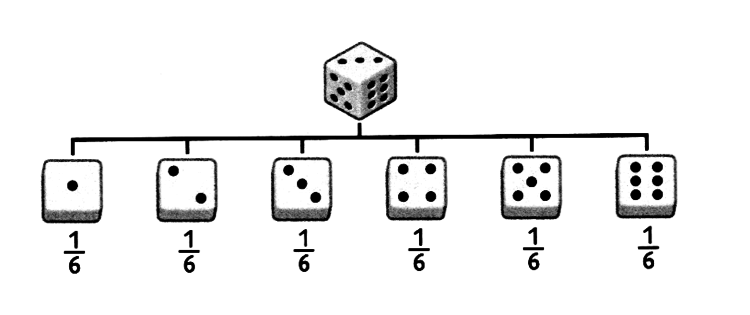
Jede Zahl wird mit einer Wahrscheinlichkeit von

$P(E) = \frac {1}{6} \approx 16,7 \%$

gewürfelt.

Betrachten wir die Wahrscheinlichkeit für das Ereignis "eine gerade Zahl würfeln":

Ereignis: "eine gerade Zahl würfeln"

Ereignismenge: $E= \{2, 4, 6\}$

$P (E) = \frac {3}{6} = \frac {1}{2}~~\widehat{=}~~50 \%$

Weitere Beispiele

Im folgenden Beispielkasten siehst du noch zwei weitere Beispiele, die dir beim Thema Laplace in Wahrscheinlichkeitsrechnung in Mathe begegnen können:

• Das Werfen einer Münze: Die Wahrscheinlichkeit für Kopf und Zahl liegt jeweils bei $50 \%$
• Das Drehen dieses Glücksrades: Jedes Feld hat eine Wahrscheinlichkeit von $ \frac {1}{6} \approx 16,7 \%$

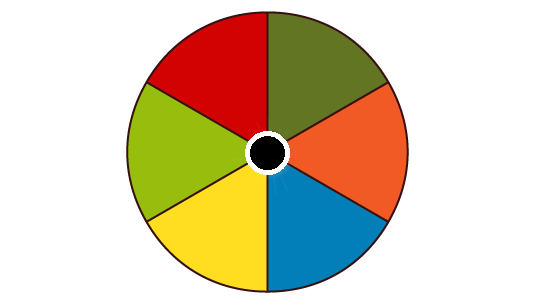
Schauen wir uns einmal an, welche Art von Zufallsversuch kein Laplace-Experiment ist. Es gibt einige Zufallsversuche, bei denen nicht alle möglichen Ergebnisse die gleiche Wahrscheinlichkeit haben.

Dazu gehören beispielsweise Würfel, bei denen eine bestimmte Zahl auf mehr als einer Seite abgebildet ist oder das Werfen einer Reißzwecke, die auf Grund ihrer Form nicht auf jeder Seite gleich wahrscheinlich liegen bleibt.

Nun weißt du, was ein Laplace-Experiment in Mathe ist, welche Regeln bei Laplace gelten und wie du die jeweiligen Wahrscheinlichkeiten bestimmen kannst. Vertiefe dein Wissen zu Laplace und Wahrscheinlichkeit in unseren Aufgaben . Dabei wünschen wir dir viel Spaß und Erfolg!

Dein Autorenteam für Mathematik: Simon Wirth und Fabian Serwitzki

Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!

Teste dein Wissen!

Was ist ein Laplace-Experiment?

Ein Los aus einem Topf ziehen mit 33 Gewinnen und 33 Nieten

Ein Los aus einem Topf ziehen mit 8 Gewinnen und 20 Nieten

Schreiben einer Klassenarbeit

Welche Rechenregel gilt bei einem Laplace-Versuch?

$P (E) = \frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ der\ möglichen\ Ergebnisse}$

$P (E) = \frac {Anzahl\ der\ möglichen\ Ergebnisse}{Anzahl\ der\ gewünschten\ Ergebnisse}$

$P (E) = \frac {Anzahl\ der\ möglichen\ Ergebnisse}{Anzahl\ der\ gewünschten\ Ergebnisse} \cdot 100\ %$

Markiere die richtigen Aussagen!

Die Wahrscheinlichkeit eine 3 zu treffen liegt bei 25%.

Es handelt sich bei dem Versuch um kein Laplace Experiment.

Das Werfen einer Münze ist ein Laplace Experiment.

Was ist kein Laplace-Experiment?

Wahl zum Klassensprecher

Werfen eines Würfels

Ziehen einer Karte aus einem Kartenspiel

Hol dir Hilfe beim Studienkreis!

Selbst-Lernportal Online

Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal . Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!

• Online-Chat 14-20 Uhr
• 700 Lerntexte & Videos
• Über 250.000 Übungsaufgaben

Jetzt kostenlos entdecken

Einzelnachhilfe Online

Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!

• Online-Nachhilfe
• Zum Wunschtermin
• Geprüfte Mathe-Nachhilfelehrer

Gratis Probestunde

• Nachhilfe in deiner Nähe

Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.

Unsere Kunden über den Studienkreis

Weitere erklärungen & übungen zum thema.

Wir sind durchgehend für dich erreichbar

Jetzt registrieren und direkt kostenlos weiterlernen!

Dein Gratis-Lernpaket:

• Lern-Bibliothek: 1 Tag Gratis-Zugang
• Hausaufgaben-Soforthilfe: 15 Gratis-Minuten
• Nachhilfe-Probestunden gratis

Falls du vom Studienkreis keine weiteren Informationen mehr erhalten möchtest, kannst du uns dies jederzeit mit Wirkung in die Zukunft an die E-Mail-Adresse [email protected] mitteilen.

Wir haben dir eine E-Mail zur Festlegung deines Passworts an geschickt.

• Öffne die E-Mail und klicke auf den Link zur Festlegung deines Passworts.
• Leg dein Passwort fest und du kannst sofort weiterlernen.

Keine E-Mail erhalten? Schaue bitte in deinem Spam-Ordner, Werbung-Ordner nach oder E-Mail erneut senden.

Die E-Mail wurde erfolgreich versendet.

Beim Versand der E-Mail ist ein Fehler aufgetreten.

• Unverbindlich und kostenlos in 2 Probestunden testen
• Sichere Notenverbesserung durch top Lehrkräfte
• Innovativstes Lernpaket: App, Hausaufgaben Live-Chat uvm.

Bitte wählen Sie einen Studienkreis in Ihrer Nähe aus.

Fordern Sie Ihren Gutschein für 2 gratis Probestunden & unverbindliche Beratung an.

Bitte geben Sie hier Ihre Kontaktdaten ein.

Die Studienkreisleitung Ihres Standorts wird sich mit Ihnen in Verbindung setzen um einen Beratungstermin zu vereinbaren falls Sie dies noch nicht online getan haben.

Vielen Dank für Ihr Interesse!

Wir haben Ihnen eine E-Mail geschickt. Der von Ihnen ausgewählte Studienkreis wird sich schnellstmöglich mit Ihnen in Verbindung setzen und Sie beraten.

• Französisch
• Mittelschule + Förderschule

Ihr Warenkorb ist leer.

Mathe, 8. Klasse

Laplace-experimente.

Arbeitsblätter mit Übungen und Aufgaben zum Thema Laplace-Experimente für Mathe in der 8. Klasse am Gymnasium - mit Lösungen!

Was ist ein Zufallsexperiment?

Experiment, deren Ergebnis zufällig passieren, also nicht vorhersagbar sind, nennt man Zufallsexperimente. Beispiele hierfür sind das Werfen eines Würfels oder einer Münze. Alle möglichen Ergebnisse eines solchen Zufallsexperimentes fasst man in der Ergebnismenge Ω zusammen.

Erkennungsmerkmale eines Zufallsexperimentes sind:

• Es wird genau ein Ergebnis von mehreren möglichen Ergebnissen eintreten.
• Es lässt sich nicht vorhersagen, welches davon eintreten wird.  

Die möglichen Ergebnisse eines Zufallsexperiments lassen sich durch ein Baumdiagramm übersichtlich darstellen.

Was ist der Unterschied zwischen Ergebnis und Ereignis?

Werden verschiedene Ergebnisse eines Experiments zusammengefasst, so erhält man ein Ereignis E . Alle Ergebnisse, die zum Ereignis E gehören, nennt man dann günstige Ergebnisse . Zum Beispiel kann man beim Werfen eines Würfels das Ereignis E „nur gerade Zahlen“ betrachten: E = {2, 4, 6}. Die Ergebnisse 2, 4 und 6 sind dann für das Ereignis E günstige Ergebnisse.

Wie kombiniert man verschiedene Ereignisse?

Sollen zwei Ereignisse E1 und E2 gleichzeitig eintreten, so schreibt man E1 ∩ E2 („E1 geschnitten mit E2“). Sollen Ereignis E1 oder E2 oder beide eintreten, so schreibt man E1 ∪ E2 („E1 vereinigt mit E2“).

Dies kann man sehr anschaulich bildlich mit einem Mengendiagramm darstellen:

Welche Spezialfälle gibt es für Ereignisse?

• Ein Ereignis, für das alle Ergebnisse günstig sind, heißt sicheres Ereignis .
• Ein Ereignis, welches nicht eintreten kann, heißt unmögliches Ereignis .
• Alle für ein Ereignis E ungünstigen Ergebnisse bilden das Gegenereignis E   von E.

Was sind relative und absolute Häufigkeit?

Man unterscheidet dabei die absolute von der relativen Häufigkeit von Ergebnissen. Die absolute Häufigkeit bezeichnet die Anzahl, wie oft ein Ergebnis eintritt. Die relative Häufigkeit beschreibt, wie oft ein Ergebnis im Verhältnis zur Gesamtzahl der Durchführungen des Experimentes auftritt. Sie wird oft in Prozent oder als Dezimalbruch angegeben:

Am Beispiel des 10-maligen Werfens eines Würfels lässt sich dies verdeutlichen:

Absolute Häufigkeit: Wie oft werfe ich dabei eine 6? Relative Häufigkeit: Wie oft werfe ich im Verhältnis zu 10 Würfen eine 6

Zu Erfassung des Zufallsexperimentes kann eine Strichliste verwendet werden. Diese sieht für das obige Experiment zum Beispiel so aus:

Was ist eine „Wahrscheinlichkeit“?

Bei Zufallsexperimenten kann man das genaue Ergebnis zwar nicht vorhersagen, aber man kann eine Wahrscheinlichkeit angeben, wie hoch die Chance ist, dass ein Ereignis eintritt.

Zum Beispiel erwartet man beim Werfen eines fairen Würfels, dass in ungefähr 1/6 aller Würfe die Augenzahl vier auftritt.

• Die Wahrscheinlichkeit ist eine Zahl zwischen 0 und 1, die oft in Prozent angegeben wird
• Eine Wahrscheinlichkeit von 0% bedeutet, dass ein Ergebnis nicht eintreten kann
• Eine Wahrscheinlichkeit von 100% bedeutet, dass ein Ergebnis sicher eintritt

Was besagt das Empirische Gesetz der großen Zahlen?

Wird ein Zufallsexperiment sehr oft wiederholt, stabilisieren sich für jedes Ergebnis die relativen Häufigkeiten auf einen bestimmten Wert. Man erwartet, dass dieser Wert nahe bei der tatsächlichen Wahrscheinlichkeit des Ergebnisses liegt.

Was beschreibt das Zählprinzip beim Baumdiagramm?

Baumdiagramme helfen, Situationen übersichtlich darzustellen.

Das Zählprinzip besagt:

Die Gesamtzahl der verschiedenen Möglichkeiten entspricht dem Produkt der Anzahlen der verschiedenen Möglichkeiten in den einzelnen Stufen beim Baumdiagramm.

Beispiel: Auf einer Speisekarte gibt es 2 Vorspeisen, 3 Hauptspeisen und 3 Nachspeisen zur Auswahl. Wie viele verschiedene dreigängige Menüs lassen sich somit zusammenstellen?

Es gibt insgesamt 2·3·3 = 18 verschiedene Möglichkeiten!

Was ist ein Laplace-Experiment?

Zufallsexperimente, bei denen jedes Ergebnis gleich wahrscheinlich ist, nennt man Laplace-Experimente. Sind bei einem Laplace-Experiment n verschiedene Ergebnisse möglich, beträgt die Wahrscheinlichkeit für jedes einzelne Ergebnis1n.

Die Wahrscheinlichkeit eines Ereignisses E kann bei Laplace-Experimenten wie folgt berechnet werden:

• Begriffe wie Ergebnis, Ereignis, Zufallsexperiment, Wahrscheinlichkeit, Laplace-Experiment kennen
• Passende Baumdiagramme erstellen und interpretieren
• Wahrscheinlichkeiten berechnen
• Mit verschiedenen Diagrammen umgehen
• Anwendungsbeispiele für Zufallsexperimente verstehen und kennen
• Beispiele nennen und erläutern
• Baumdiagramme und Vierfeldertafeln erstellen
• Rechnungen mit Wahrscheinlichkeiten durchführen
• Säulendiagramme erstellen

Kostenlose Arbeitsblätter zu Laplace-Experimenten

Laplace-experimente 1, laplace-experimente 2, laplace-experimente 3, laplace-experimente 4, laplace-experimente 5, laplace-experimente 6.

• Report an issue

Laplace probability

Experiments in which all results are equally likely are called Laplace experiments .

The probability of an event is calculated in a Laplace experiment with the formula:

$|E| ...$ Number of results where $E$ occurs $|\Omega| ...$ Total number of results

Examples of Laplace experiments are the throwing of a coin, a dice or the turning of a wheel of fortune with fields of equal size.

A dice is thrown. Your are interested in the probability of an even number.

Sample space : $\Omega=\{1,2,3,4,5,6\}$ Event : $E=\{2, 4, 6\}$ Probability: $P(E) = \frac{|E|}{|\Omega|}$ $=\frac{3}{6}$

Non-Laplace experiment

In non-Laplace experiments , the probabilities for each possible outcome can not be determined by e.g. symmetry considerations or the like. However, after many experiments have been carried out, estimates of the probabilities can be determined.

Examples of non-Laplace experiments are the throwing of thumbtacks, a LEGO stone or a crown cork. It is not exactly possible to say which event occurs with which probability.

Laplace-Experiment

In diesem Kapitel schauen wir uns an, was ein Laplace-Experiment ist.

Erforderliches Vorwissen

• Was ist ein Zufallsexperiment ?
• Was ist ein Ereignis ?
• Was ist ein Elementarereignis ?

Definition 

Ein Laplace-Experiment ist ein spezielles Zufallsexperiment:

Ein Zufallsexperiment heißt Laplace-Experiment , wenn alle Elementarereignisse die gleiche Wahrscheinlichkeit besitzen.

Beispiel 1  

Werfen eines Würfels

Beispiel 2  

Werfen einer Münze

Beispiel 3  

Ziehen einer Kugel aus einer Urne

Beispiel 4  

Ziehen einer Karte aus einem Kartenspiel

Beispiel 5  

Lotto (z. B. 6 aus 49)

Beispiel 6  

Toto (Sportwetten)

Die oben genannten Glücksspiele behandelt man im Allgemeinen idealisiert als Laplace-Experimente.

Laplace-Würfel vs. Laplace-Münze

Dass es sich um ein Laplace-Experiment handelt, verrät bereits häufig die Aufgabenstellung. Oft ist nämlich von einem Laplace-Würfel oder Ähnlichem die Rede. Ein Laplace-Würfel (L-Würfel) ist ein idealer Würfel, bei dem das Auftreten jeder Augenzahl gleich wahrscheinlich ist. Eine ideale Münze bezeichnet man dementsprechend auch als Laplace-Münze (L-Münze).

Laplace-Wahrscheinlichkeit 

Die Wahrscheinlichkeit eines Ereignisses in einem Laplace-Experiment heißt Laplace-Wahrscheinlichkeit .

Formel 

$$ P(E) = \frac{|E|}{|\Omega|} $$

In Worten: Die Wahrscheinlichkeit eines Ereignisses $E$ eines Laplace-Experiments ist gleich dem Quotienten aus den Mächtigkeiten des Ereignisses $E$ und des Ergebnisraums $\Omega$ .

• $P(E)$ = Wahrscheinlichkeit des Ereignisses $E$
• $|E|$ = Anzahl der Elementarereignisse, bei denen $E$ eintritt
• $|\Omega|$ = Anzahl aller überhaupt möglichen Elementarereignisse

Die Formel zur Berechnung der Laplace-Wahrscheinlichkeit gilt nur, wenn die Elementarereignisse bei dem jeweiligen Experiment gleich wahrscheinlich sind. Hat man jedoch Grund zur Annahme, dass die Elementarereignisse nicht gleich wahrscheinlich sind, darf die Formel nicht angewendet werden!

Laplace-Wahrscheinlichkeit berechnen 

Anzahl aller überhaupt möglichen Elementarereignisse berechnen

Anzahl der Elementarereignisse berechnen, bei denen $\boldsymbol{E}$ eintritt

Laplace-Wahrscheinlichkeit berechnen

Für den 1. und 2. Schritt braucht man die Kombinatorik .

Beispiel 7  

Eine Laplace-Münze wird dreimal geworfen.

Wie groß ist die Wahrscheinlichkeit, dreimal $K$ zu werfen?

Variation mit Wiederholung : $n^k$

$$ |\Omega|= n^k = 2^3 = {\colorbox{orange}{$8$}} $$

Zusatzinformation

$$ \Omega = \{KKK, KKZ, KZK, ZKK, ZZK, ZKZ, KZZ, ZZZ\} $$

Kombination ohne Wiederholung : $\binom{n}{k}$

$$ |A| = \binom{3}{3} = {\colorbox{yellow}{$1$}} $$

$$ A = \{KKK\} $$

$$ P(A) = \frac{|A|}{|\Omega|} = \frac{{\colorbox{yellow}{$1$}}}{{\colorbox{orange}{$8$}}} $$

Beispiel 8  

Wie groß ist die Wahrscheinlichkeit, mindestens zweimal $K$ zu werfen?

$$ |B| = \binom{3}{2} + \binom{3}{3} = 3 + 1 = {\colorbox{yellow}{$4$}} $$

$$ B = \{KKZ, KZK, ZKK, \: KKK\} $$

$$ P(B) = \frac{|B|}{|\Omega|} = \frac{{\colorbox{yellow}{$4$}}}{{\colorbox{orange}{$8$}}} = \frac{1}{2} $$

Beispiel 9  

Wie groß ist die Wahrscheinlichkeit, mindestens einmal $K$ zu werfen?

$$ |C| = \binom{3}{1} + \binom{3}{2} + \binom{3}{3} = 3 + 3 + 1 = {\colorbox{yellow}{$7$}} $$

$$ C = \{ZZK, ZKZ, KZZ, \: KZZ, KZK, ZKK, \: KKK\} $$

$$ P(C) = \frac{|C|}{|\Omega|} = \frac{{\colorbox{yellow}{$7$}}}{{\colorbox{orange}{$8$}}} $$

In obigen Beispielen hätte man die Mengen von $E$ und $\Omega$ auch – ohne Anwendung kombinatorischer Formeln – einfach abzählen können. In den meisten Aufgaben sind die Mengen allerdings so groß, dass ein Abzählen nicht möglich ist. Aus diesem Grund wurde auch in diesen einfachen Beispielen zu Übungszwecken auf die Kombinatorik zurückgegriffen.

Probestunde sichern

Laplace-Experiment – Mathe

Ein Laplace-Experiment ist ein Zufallsversuch, bei dem alle Elementarereignisse die gleiche Wahrscheinlichkeit haben. Erfahre, wie die Laplace-Formel angewendet wird und welche Bedingungen erfüllt sein müssen. Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Laplace-Experiment

• Das Laplace-Experiment im Überblick

Laplace-Experiment – Erklärung

Laplace-experiment – definition, laplace-experiment – formel, laplace-experiment – zusammenfassung der eigenschaften.

• Laplace-Experiment –  Beispiele

Laplace-Experiment – Urne

Laplace-experiment – würfel, nicht-laplace-experimente – beispiele, häufig gestellte fragen zum thema laplace-experiment, das quiz zum thema: laplace-experiment.

Was ist ein Laplace-Experiment?

Frage 1 von 5

Wie lautet die Laplace-Regel?

Frage 2 von 5

Wie erkenne ich ein Laplace-Experiment?

Frage 3 von 5

Was sind die Eigenschaften eines Laplace-Experiments?

Frage 4 von 5

Was ist die Laplace-Regel?

Frage 5 von 5

Das Laplace-Experiment  im Überblick

• Ein Laplace-Experiment ist ein Zufallsversuch, bei dem alle Elementarereignisse die gleiche Wahrscheinlichkeit haben.

Quelle sofatutor.com

Wie willst du heute lernen?

Bei dem Laplace-Experiment handelt es sich um einen Zufallsversuch mit besonderen Merkmalen . 

Zufallsversuch – Definition Als Zufallsversuch ( Zufallsexperiment) wird in Mathe ein Vorgang bezeichnet, der ohne Veränderung wiederholt werden kann. Der Ausgang des Experiments ist dabei unter den bekannten Möglichkeiten nicht vorhersehbar. Ein Beispiel für ein Zufallsexperiment  ist das Würfeln mit einem immer gleichen Würfel . Hier wissen wir, dass das Ergebnis eine der Zahlen des Würfels ist. Welches Ergebnis die einzelnen Würfe liefern, ist vorab jedoch nicht bekannt.

Ein Zufallsversuch, bei dem alle Elementarereignisse die gleiche Wahrscheinlichkeit haben, wird als Laplace-Experiment ( Laplace-Versuch ) bezeichnet. Das bedeutet, dass ein Laplace-Experiment , neben den Voraussetzungen für den Zufallsversuch, die Bedingung erfüllt, dass alle Elementarereignisse gleich wahrscheinlich sind. 

Mit der Laplace-Formel kann die Wahrscheinlichkeit einzelner Ereignisse berechnet werden. Diese Formel wird auch als Laplace-Regel bezeichnet. Dabei wird die Anzahl der günstigen Ergebnisse durch die Anzahl der möglichen Ergebnisse geteilt.

Solche Ereignisse werden auch als zusammengesetzte Ereignisse bezeichnet, da sie aus mehreren Elementarereignissen zusammengesetzt sind. Für Elementarereignisse gibt es genau ein günstiges Ergebnis. Die Wahrscheinlichkeit für ein Elementarereignis ist damit nach der Laplace-Formel:

Der Laplace-Versuch ist eine besondere Form der Zufallsversuche. Die folgende Tabelle zeigt, welche Eigenschaften erfüllt sein müssen, damit es sich um einen Zufallsversuch oder um einen Laplace-Versuch handelt.

Laplace-Experiment – Beispiele

Die allgemeine Formel zur Berechnung der Wahrscheinlichkeit lautet:

Als Gegenteil der Laplace-Experimente werden Zufallsexperimente bezeichnet, bei denen die Ereignisse nicht alle die gleiche Wahrscheinlichkeit besitzen. Bei diesen Experimenten kann die Laplace-Formel nicht angewandt werden. Beispiele für ein Nicht -Laplace-Experiment sind das Würfeln mit einem gezinkten Würfel oder das Werfen einer Reißzwecke, die fast immer auf den Kopf fällt.

Ein Laplace-Experiment ist ein Zufallsversuch, bei dem alle Elementarereignisse die gleiche Wahrscheinlichkeit besitzen. Das Würfeln mit einem ungezinkten Würfel ist ein Beispiel für ein Laplace-Experiment. Das Werfen einer Reißzwecke ist kein Laplace-Experiment, da sie fast immer auf dem Kopf landen wird. 

Sind bei einem Zufallsversuch die Wahrscheinlichkeiten aller Elementarereignisse gleich groß, handelt es sich um ein Laplace-Experiment.

Bei einem Laplace-Experiment können die Wahrscheinlichkeiten von Ereignissen berechnet werden, indem die Anzahl der für das Ereignis günstigen Ergebnisse durch die Anzahl aller möglichen Ergebnisse geteilt wird.

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community! Antworten abbrechen

Alle Artikel aus dem Fach Mathematik

• Wurzel ziehen
• Urnenmodell
• Was Ist parallel
• Uhrzeit lernen
• Winkelarten
• Funktionsgraphen
• Funktionsgleichung
• Sinussatz und Cosinussatz
• Absolute Häufigkeit und relative Häufigkeit, Häufigkeiten
• Baumdiagramm
• Wahrscheinlichkeitsrechnung
• Partielle Integration
• Logarithmus
• Würfel Geometrie
• Kalender Grundschule
• Scheitelpunktform
• Was ist ein Term?
• Proportionale und antiproportionale Zuordnung
• Trigonometrische Funktionen ableiten
• Winkelhalbierende
• Multiplizieren
• Pyramide berechnen
• Gewinnfunktion und Erlösfunktion
• Lagebeziehung Gerade Ebene
• Obersumme und Untersumme
• Zinsrechnung
• Vektorrechnung
• Römische Zahlen
• Volumen und Volumen berechnen
• Längeneinheiten
• Nullstellen berechnen
• Transformation Mathe
• Prozentuale Veränderung berechnen
• Kreuzprodukt
• Ganzrationale Funktion
• Vorgänger Und Nachfolger
• Balken- und Säulendiagramm
• Additionstheoreme
• Rechnen mit Geld
• Lineare Ungleichungen
• Formel umstellen
• Quadratische Funktionen
• Vollständige Induktion
• Steigungswinkel berechnen
• Binomische Formeln
• Geradenschar
• Temperatur Einheiten
• Exponentielles Wachstum
• Brüche Kürzen und Brüche Erweitern
• Brüche dividieren
• Quadratische Gleichungen
• Prozentsatz
• Gegenwahrscheinlichkeit
• Kegel berechnen
• Prozentrechnung
• Kathetensatz und Höhensatz
• Normalverteilung
• Exponentialfunktion
• Binomialverteilung
• Brüche multiplizieren
• Assoziativgesetz
• Flächeninhalt
• Ableitungsfunktionen
• Polynomdivision
• Hunderterfeld
• Koordinatensystem
• Laplace-Experiment
• Orthogonalität
• Minus Mal Minus
• Quadernetze
• Würfelnetze
• Was sind Flächen?
• Quadratische Ergänzung
• Rationale Zahlen
• Mittlere Änderungsrate
• Geometrie und geometrische Grundbegriffe
• Umfang und Umfang berechnen
• Lineare Funktionen
• Erwartungswert
• Dezimalbruch und Dezimalbruch In Prozent
• Grundrechenarten
• Das kleine Einmaleins und das große Einmaleins
• Maßeinheiten
• Oberfläche Kugel und Volumen Kugel
• Quotientenregel
• Vektor und was ist ein Vektor
• Vierfeldertafel
• Dreiecke & Dreiecksarten
• Kongruenz Mathe
• Rotationskörper
• Primfaktorzerlegung
• Satz vom Nullprodukt
• Kommutativgesetz
• Größer-als- und Kleiner-als-Zeichen
• Stammfunktion
• Terme und Gleichungen
• Flächeninhalt Dreieck
• Quadratzahlen
• Kettenregel
• Lageparameter
• Ausklammern und Ausmultiplizieren
• Punktsymmetrie
• Trigonometrie
• Was ist eine Kante?
• Kreiszahl Pi
• Magisches Quadrat
• Parallelogramm
• Kreis und Kreisumfang
• Reelle und irrationale Zahlen
• Teilbarkeitsregeln
• Produktregel
• e-Funktion ableiten
• Kleinstes gemeinsames Vielfaches und kgV berechnen
• Zeiteinheiten
• Umkehraufgaben
• Winkelfunktion
• Bedingte Wahrscheinlichkeit
• Gleichsetzungsverfahren
• Gewichte umrechnen
• Zahlen in Worten
• Haus der Vierecke
• Drachenviereck Flächeninhalt
• Brüche addieren & subtrahieren
• Bogenmaß & Gradmaß
• Geradengleichung
• Potenzgesetze
• Distributivgesetz
• Satz des Thales
• Mitternachtsformel
• Natürliche Zahlen
• Größter gemeinsamer Teiler (ggT)
• Sinusfunktion
• Extremwertaufgaben
• Additionsverfahren

Ähnliche Themen

Hol dir alle Funktionen.

Mit unserer App hast du immer und überall Zugriff auf alle Funktionen.

Get the best learning hacks!

Lorem ipsum dolor sit amet, consetetur sadipscing elitr, sed diam nonumy eirmod tempor invidunt ut labore et dolore magna aliquyam erat, sed diam voluptua.

Laplace-Experiment & Laplace-Wahrscheinlichkeit

Hast du dich schon einmal gefragt, wie du die Wahrscheinlichkeit von bestimmten Ereignissen berechnest? Die Laplace-Wahrscheinlichkeit bietet eine der wichtigsten Möglichkeiten, um solche Wahrscheinlichkeiten zu bestimmen.

Aber welche Voraussetzungen müssen erfüllt sein, damit du mit der Laplace-Wahrscheinlichkeit rechnen darfst?

simpleclub zeigt dir alles, was du über Laplace-Experimente und Laplace-Wahrscheinlichkeiten wissen musst.

Laplace-Experiment einfach erklärt

Ein prototypisches Beispiel für ein Laplace-Experiment ist das einmalige Werfen mit einem Würfel.

Ein Laplace-Experiment ist einfach ein Zufallsexperiment mit der Zusatzbedingung, dass alle Ergebnisse die gleiche Wahrscheinlichkeit haben.

Das Würfeln ist zum Beispiel ein Laplace-Experiment , da es ein normales Zufallsexperiment ist und zusätzlich alle Zahlen mit der gleichen Wahrscheinlichkeit auftreten.

Laplace-Wahrscheinlichkeit

Mit der Laplace-Wahrscheinlichkeit berechnest du die Wahrscheinlichkeit eines beliebigen Ereignisses A A A A bei einem Laplace-Experiment .

Dabei teilst du die Anzahl der Elemente , die zu diesem Ereignis führen, durch die Gesamtanzahl an Möglichkeiten.

Laplace-Experiment Definition

Ein Laplace Experiment ist ein Zufallsexperiment, bei dem alle Ergebnisse dieselbe Wahrscheinlichkeit haben.

Laplace-Wahrscheinlichkeit Definition

Die Laplace-Wahrscheinlichkeit berechnet die Wahrscheinlichkeit eines bestimmten Ereignisses A A A A durch:

Laplace-Experiment

Ein Laplace Experiment ist also nichts anderes als ein normales Zufallsexperiment mit zusätzlicher Einschränkung.

Bei einem Zufallsexperiment sind immer drei Merkmale erfüllt:

• Der Ausgang des Zufallsexperiments ist nicht vorhersagbar .
• Das Zufallsexperiment hat mehrere Ausgänge (sogenannte Ergebnisse).
• Das Zufallsexperiment kann beliebig oft wiederholt werden.

Für ein Laplace-Experiment muss zusätzlich gegeben sein:

Dies vereinfacht das Rechnen mit Wahrscheinlichkeiten erheblich. Deshalb werden dir Laplace Experimente in der Schule häufig begegnen.

Typische Alltagsbeispiele sind das Werfen eines normalen Würfels, das Ziehen einer bestimmten Karte aus einem Kartendeck oder andere Situationen, in denen der Ausgang aller Ergebnisse genau gleich wahrscheinlich ist.

Alle Zufallsexperimente, bei denen nicht alle Ergebnisse die gleiche Wahrscheinlichkeit haben, sind keine Laplace Experimente !

Zum Beispiel ist das Drehen des folgenden Glücksrads kein Laplace-Experiment, da nicht alle Ergebnisse die gleiche Wahrscheinlichkeit haben.

Berechnung der Laplace-Wahrscheinlichkeit

Du kannst die Wahrscheinlichkeit eines Laplace-Experiments berechnen, wenn du die Anzahl der Ergebnisse zu einem Ereignis durch die Gesamtanzahl an Möglichkeiten teilst.

Beim einmaligen Werfen eines handelsüblichen Würfels gehören zu dem Ereignis G G G G : Es wird eine gerade Zahl gewürfelt die Ergebnisse 2 2 2 2 , 4 4 4 4 und 6 6 6 6 . Die Anzahl an Möglichkeiten zu dem Ereignis G G G G sind also 3 3 3 3 .

Mathematisch ausgedrückt ist das die Mächtigkeit des Ereignisses G G G G . Du sagst also Ereignis G G G G besitzt die Mächtigkeit 3 3 3 3 .

Das schreibst du dann mit Betragsstrichen um das Ereignis:

Es können insgesamt die Zahlen 1 1 1 1 bis 6 6 6 6 gewürfelt werden.

Die Anzahl aller Ergebnisse im Ergebnisraum ist die Mächtigkeit des Ergebnisraum .

Du kannst die Wahrscheinlichkeit des Ereignisses G G G G , also P(G) P ( G ) P(G) P ( G ) , nun durch die Laplace-Wahrscheinlichkeit berechnen. Dazu teilst du die Mächtigkeit des Ereignisses durch die Mächtigkeit des Ergebnisraums .

Mit der Karteikartenfunktion kannst du deine Vokabeln, Definitionen oder andere Themen, die du auswendig lernen musst, einfach einscannen.

Pasch würfeln

Jan und ein Freund würfeln in einem Café mit zwei Würfeln darum, wer von ihnen den nächsten Kaffee bezahlen muss.

Bei einem Pasch (beide Würfel zeigen dieselbe Augenzahl) ist Jan an der Reihe, bei allen anderen Würfen muss sein Freund bezahlen.

Berechne die Wahrscheinlichkeit , dass Jan den nächsten Kaffee bezahlen muss.

Es handelt sich um ein Laplace Experiment , da alle möglichen Würfe gleich wahrscheinlich sind.

Es gibt 6 Möglichkeiten , einen Pasch zu würfeln (also 6 gewünschte Ergebnisse ):

Insgesamt gibt es 36 mögliche Ergebnisse , da mit zwei Würfeln 36 verschiedene Kombinationen möglich sind:

Du berechnest nun die Wahrscheinlichkeit dafür, dass Jan Kaffee holen muss, indem du die Anzahl der gewünschten Ergebnisse (einen Pasch) durch die Anzahl aller möglichen Ergebnisse teilst:

Karte ziehen

In einem gewöhnlichen Skatdeck befinden sich insgesamt 32 Karten .

Wie hoch ist die Wahrscheinlichkeit bei einmaligem Ziehen einen Buben aus dem Deck zu ziehen?

Wieder handelt es sich um ein Laplace Experiment , da die Wahrscheinlichkeit eine bestimmte Karte zu ziehen bei jeder Karte genau gleich groß ist.

Es gibt vier Buben in dem Kartendeck, also ist dies auch die Anzahl der gewünschten Ergebnisse :

Insgesamt sind 32 Karten im Kartendeck, also können auch 32 verschiedene Karten gezogen werden. Somit gibt es 32 mögliche Ergebnisse :

Nun berechnest du die Gesamtwahrscheinlichkeit einen Buben zu ziehen , indem du die Anzahl der gewünschten Ergebnisse (ein Bube wird gezogen) durch die Anzahl aller möglichen Ergebnisse teilst:

Zusammenfassung

Ein Laplace-Experiment ist ein Zufallsexperiment , bei dem zusätzlich alle Ergebnisse die gleiche Wahrscheinlichkeit besitzen.

Bei der Laplace-Wahrscheinlichkeit berechnest du die Wahrscheinlichkeit eines Ereignis A A A A , indem du die Anzahl der günstigen Möglichkeiten durch die Gesamtmöglichkeiten teilst.

simpleclub ist am besten in der App.

Mit unserer App hast du immer und überall Zugriff auf: Lernvideos, Erklärungen mit interaktiven Animationen, Übungsaufgaben, Karteikarten, individuelle Lernpläne uvm.

Related topics

Mittelwert (arithmetisches mittel), erwartungswert, bedingte wahrscheinlichkeit, jetzt simpleclub azubi holen.

Mit simpleclub Azubi bekommst du Vollzugang zur App: Wir bereiten dich in deiner Ausbildung optimal auf deine Prüfungen in der Berufsschule vor. Von Ausbilder*innen empfohlen.

Lernen leicht gemacht

Laplace-Experiment – so verstehst Du es einwandfrei

Ein Laplace-Experiment – im Mathematikunterricht begegnet man diesem Thema im Rahmen der Stochastik. Doch was versteht man eigentlich genau unter einem Laplace-Versuch ? Die Antwort zu dieser Frage findest Du schnell und einfach im folgenden Artikel.

Im Folgenden siehst Du ,…

– … was überhaupt ein Laplace-Experiment ist, – … was Nicht-Laplace-Experimente dementsprechend sind, – … Beispiele zu Laplace-Experimenten – … und schließlich Aufgaben zu Laplace-Experimenten zum Üben.

Laplace-Experiment Definition – so klappt das ganz simpel

Ein Laplace-Experiment ist ein Zufallsversuch mit besonderen Bedingungen. Es wurde nach dem Mathematiker Pierre-Simon Laplace benannt, der sich in seinem Leben u.a. mit der Wahrscheinlichkeitstheorie auseinandergesetzt hat. Welche Bedingungen ein Laplace-Versuch  erfüllen muss, lernst Du im folgenden Kapitel.

Was ist ein Laplace-Experiment?

Ein Laplace-Experiment ist ein Zufallsexperiment, bei dem alle Ereignisse, die eintreten können, genau dieselbe Wahrscheinlichkeit haben.

Um die Wahrscheinlichkeit von Ereignissen solcher Zufallsexperimente berechnen zu können, verwendet man die sogenannte “Laplace-Formel”.

Laplace-Formel:

Nicht-Laplace-Experimente

Nicht-Laplace-Experimente sind hingegen Zufallsexperimente, bei denen alle Ereignisse, die auftreten können, nicht dieselbe Wahrscheinlichkeit haben.

Beispiele für solche Nicht-Laplace-Experimente sind das Werfen einer Reißzwecke oder eines gezinkten Würfels.

Laplace-Experiment Beispiele – Schritt für Schritt erklärt

Betrachten wir zuerst einen normalen Würfel, der einmal geworfen wird.

Dieser Würfel hat sechs komplett gleich große Seiten mit sechs verschiedenen Zahlen.

Die Wahrscheinlichkeit, eine bestimmte Zahl bei einem Wurf zu würfeln, liegt also immer bei einem Sechstel .

Somit liegt in diesem Fall ein Laplace-Experiment vor.

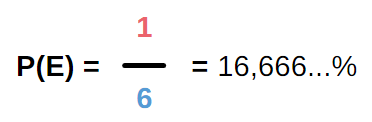
Was wäre aber, wenn man möchte, dass ein bestimmtes Ereignis auftritt?

Wie hoch wäre beispielsweise die Wahrscheinlichkeit, dass eine Zahl bei einmaligem Wurf gewürfelt wird, die höchstens drei beträgt?

Um diese Wahrscheinlichkeit zu berechnen, verwendet man ebenfalls die Laplace-Formel:

Es gibt drei mögliche Ereignisse, die die Bedingung der Aufgabenstellung erfüllen. Entweder wird eine 1, eine 2 oder eine 3 gewürfelt.

Das heißt, es gibt genau drei gewünschte Ereignisse, die auftreten können. Die Anzahl der möglichen Ereignisse beträgt hier immer sechs.

Der Quotient wird nach der Laplace-Formel gebildet und schon man hat das gewünschte Ergebnis.

Betrachten wir nun eine Münze, die einmal geworfen wird. Diese Münze hat zwei genau große Seiten mit je einem Symbol (“Kopf” oder “Zahl”).

Die Wahrscheinlichkeit, dass eine Seite nach einem Münzwurf oben sichtbar ist, beträgt immer 50 %. Hier liegt daher auch ein Laplace-Experiment vor.

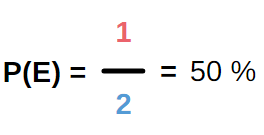
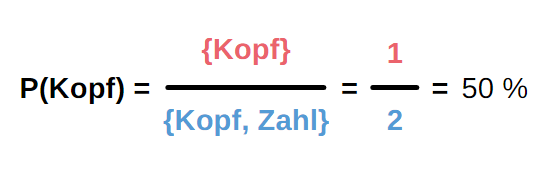
Wenn man bspw. nach einem Münzwurf “Kopf” oben sichtbar haben will, nutzt man zur Berechnung der Wahrscheinlichkeit wieder die Laplace-Formel.

Es gibt hier nur ein gewünschtes Ereignis, nämlich das, dass “Kopf” fällt.

Die Anzahl der möglichen Ereignisse ist hier immer zwei. Man bildet wieder den Quotienten und erhält das gewünschte Ergebnis.

Ein weiteres, etwas komplexeres, Beispiel ist das Casino Spiel Roulette. Die Wahrscheinlichkeit für jede Zahl auf dem Roulette Spielfeld ist genau gleich groß.

Wenn du auf eine bestimmte Farbe setzen würdest ist die 0 eine Besonderheit, weil sie die einzige Zahl ist ohne Farbe und damit immer ein Gewinn für das Casino darstellt.

Laplace-Experiment Aufgaben zum schnellen Vertiefen

Falls Du Deine erlernten Kenntnisse zum Thema “ Laplace-Experiment ” vertiefen möchtest, kannst Du hier anhand dieser Aufgaben dein erlerntes Wissen auf die Probe stellen.

Mithilfe der Lösungen kannst Du Deine Ergebnisse durch einen Klick auf das jeweilige Plus überprüfen. Weitere Aufgaben findest Du ansonsten im Link.

Aufgabe 1: Entscheide, ob es sich bei den folgenden Zufallsexperimenten um ein Laplace-Versuch  handelt!

a) Das Werfen eines normalen Würfels

Ja, da die Wahrscheinlichkeit für das Auftreten eines Ereignisses beim Wurf eines normalen Würfels immer ca. 16,67 % beträgt.

b) Das Werfen einer Reißzwecke

Nein, da die Wahrscheinlichkeiten, dass die Reißzwecke nach dem Wurf auf dem Kopf oder auf der Seite landet, nicht gleich sind.

c) Das Drehen eines Glücksrads mit drei unterschiedlich großen Feldern

Nein, da es drei unterschiedlich große Felder gibt und somit die Wahrscheinlichkeiten für das Auftreten dieser Felder nicht gleich sein können.

d) Das Drehen eines Glücksrads mit drei gleich großen Feldern

Ja, da die Felder gleich groß und somit die Wahrscheinlichkeit für das Auftreten der verschiedenen Felder gleich sind.

e) Das Werfen einer Münze

Ja, da die Wahrscheinlichkeit für das Auftreten eines Ereignisses (“Kopf” oder “Zahl”) beim Wurf einer Münze immer 50 % beträgt.

f) Das Werfen einer gezinkten Münze

Nein, da die Münze gezinkt ist und somit die Wahrscheinlichkeiten für das Auftreten eines Ereignisses (“Kopf” oder “Zahl”) nicht gleich sind.

Aufgabe 2: Du würfelst einmal einen normalen Würfel.

a) Wie hoch ist die Wahrscheinlichkeit, dass Du eine 5 würfelst?

1 — = P(5) (Anwendung der Laplace-Formel) 6

b) Wie hoch ist die Wahrscheinlichkeit, dass Du eine Zahl kleiner als 3 würfelst?

2      1 — = — = P (x < 3) (Anwendung der Laplace-Formel) 6      3

c) Wie hoch ist die Wahrscheinlichkeit, dass Du eine Zahl würfelst, die mindestens 4 beträgt?

3      1 — = — = P (x ≥ 4) (Anwendung der Laplace-Formel) 6      2

d) Wie hoch ist die Wahrscheinlichkeit, dass Du eine 2 oder eine 6 würfelst?

2      1 — = — = P (x = {2,6}) (Anwendung der Laplace-Formel) 6      3

e) Wie hoch ist die Wahrscheinlichkeit, dass Du keine 1 würfelst?

5 — = P (x ≠ 1) (Anwendung der Laplace-Formel) 6

f) Wie hoch ist die Wahrscheinlichkeit, dass Du keine 3 oder 4 würfelst?

4      2 — = — = P (x ≠ {3,4}) (Anwendung der Laplace-Formel) 6      3

Laplace-Versuch: Häufig gestellte Fragen / FAQ

Was ist ein laplace-experiment und was nicht.

Ein Laplace-Experiment ist ein Zufallsversuch, bei dem alle möglichen Ereignisse genau die gleiche Wahrscheinlichkeit haben. Nicht-Laplace-Experimente sind Zufallsversuche, bei denen alle möglichen Ereignisse nicht die gleiche Wahrscheinlichkeit haben wie bspw. der Wurf einer Reißzwecke oder eines gezinkten Würfels.

Ist ein Münzwurf ein Laplace-Experiment?

Die möglichen Ereignisse beim Münzwurf sind, dass entweder “Kopf” oder “Zahl” geworfen wird. Beide Ereignisse können mit derselben Wahrscheinlichkeit von 50 % eintreten. Daher handelt es sich hier um ein Laplace-Experiment.

Ist ein Glücksrad ein Laplace-Experiment?

Nur wenn die Wahrscheinlichkeiten für das Eintreten aller Felder auf dem Glücksrad gleich sind, handelt es sich bei einem Glücksrad um ein Laplace-Experiment.

Wie berechnet man die Laplace-Wahrscheinlichkeit?

Um die Wahrscheinlichkeit von Laplace-Versuchen zu bestimmen, nutzt man die Laplace-Formel. Dabei wird die Anzahl der gewünschten Ereignisse durch die Anzahl der möglichen Ereignisse geteilt und man erhält die Wahrscheinlichkeit für ein bestimmtes Ereignis.

Was ist die Laplace-Bedingung?

Die Laplace-Bedingung tritt ein, wenn die Standardabweichung größer als 3 ist. Die Standardabweichung dient als Maß dafür, wie weit die jeweiligen Zahlen verteilt bzw. wie weit die jeweiligen Messwerte durchschnittlich von dem Erwartungswert/Mittelwert entfernt sind.

Wir haben uns viel Mühe mit dem Artikel gegeben und freuen uns riesig, wenn du uns noch eine Sternebewertung da lässt.

Vielen dank, 4,50 von 5 sterne loading..., kommentar verfassen kommentieren abbrechen.

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

E-Mail-Adresse*

Meinen Namen, meine E-Mail-Adresse und meine Website in diesem Browser für die nächste Kommentierung speichern.

Mathe Lerntipps

Sicher und schnell Mathe lernen

Laplace Experiment

„Lasst uns eine Münze werfen.“ Hättet ihr vielleicht nicht gedacht, dass man die Wahrscheinlichkeit berechnen kann, ob im nächsten Moment Zahl oder Kopf erscheint? Dann solltet ihr unbedingt einen Blick auf das Laplace Experiment werfen.

Was ist die Laplace Regel

• Der französische Mathmatiker Pierre-Simon Laplace (1749 – 1827) machte Entdeckungen in der Wahrscheinlichkeitsrechnung, die in der modernen Mathematik heute unverzichtbar sind. Er hat herausgefunden, dass bei manchen Zufallsexperimenten alle Ergebnisse gleichwahrscheinlich sind. Bei einem Münzwurf ist es zum Beispiel gleichwahrscheinlich, auf welcher Seite die Münze landet – Kopf oder Zahl. Zufallsexperimente wie diese nennt man daher nach dem französischen Mathematiker Laplace-Zufallsexperimente

Laplace Wahrscheinlichkeit berechnen

Vorgehensweise

• Anzahl aller überhaupt möglichen Elementarereignisse berechnen
•  Anzahl der Elementarereignisse berechnen, bei denen E eintritt
• Laplace-Wahrscheinlichkeit berechnen

Formel Laplace Experiment

Einführung in das Laplace Experiment

Natürlich gehen wir davon aus, dass in Wirklichkeit die Karten gezinkt und Münzen und Würfel manipuliert sein können. Dennoch brauchen wir für die Berechnung und den Versuch eine exaktere Form der Wirklichkeit.

Einen Laplace Versuch gibt es nur in der Theorie. Wir betrachten das Münzbeispiel.

Wenn Du eine reale Münze wirfst, kann sie auf die eine oder andere Seite fallen. Da aber eine Münze mechanisch hergestellt ist, kann sie Unregelmäßigkeiten aufweisen, die dazu führen, dass sie öfter auf die eine Seite fällt als auf die andere. Außerdem kann eine Münze auch in sehr seltenen Fällen auf der Kante stehenbleiben.

Laplace hat sich für seine Wahrscheinlichkeitsrechnung eine Münze vorgestellt, die wirklich genau zu 50% auf der einen oder anderen Seite zu liegen kommt. Außerdem fällt die Laplace Münze nie auf die Kante. Es handelt sich also um das theoretische Idealbild einer Münze.

Dementsprechend gibt es dann auch andere Lapalace-Zufallsgeräte (z.B. Würfel).

Wird ein Zufallsexperiment mit einer endlichen Ergebnismenge E hinreichend oft wiederholt und zeigt sich dabei, daß keines der Elementarereignisse gegenüber einem anderen bevorzugt auftritt, so werden alle Ereignisse stets näherungsweise gleich häufig auftreten und wir sprechen von einem Laplace-Experiment

Wann die Laplace-Formel nicht gilt

Beim Münz- und Würfelwurf funktioniert die Anwendung der Laplace-Formel prima. Bei vielen anderen Zufallsexperimenten allerdings nicht. Sie kann nur dann angewendet werden, wenn alle Elementarereignisse die selbe Eintrittswahrscheinlichkeit haben. Bei der Münze und beim Würfel ist das gegeben: Per Zufall erscheint eine der Seiten und keine hat eine höhere Wahrscheinlichkeit als irgendeine andere Seite. Bereits bei einem gezinkten Würfel, der z. B. in 50% aller Fälle eine 6 ergibt und in 50% aller Fälle eine Augenzahl zwischen 1 und 5 versagt die Laplace-Formel.

Wieso kann die Formel nun nicht auf solche Zufallsexperimente angewendet werden?

Das liegt daran, dass in der Formel nur die Anzahlen eine Rolle spielen: Die Anzahl aller gesuchten Elementarereignisse wird durch die Anzahl aller möglichen Elementarereignisse geteilt. Verwendet man nur die Anzahlswerte, dann setzt man voraus, dass die Eintrittswahrscheinlichkeit jedes einzelnen Elementarereignisses gleich ist — andernfalls müssten auch die Eintrittswahrscheinlichkeiten der Elementarereignisse in der Formel auftauchen. ⇒ Die Laplace-Formel darf nur dann verwendet werden, wenn jedes Elementarereignis die selbe Eintrittswahrscheinlichkeit hat (siehe z. B. Würfel oder Münzwurf)

Bei den folgenden Experimenten und Ereignissen handelt es sich um das Laplace Experiment:

• Münze werfen
• Karte ziehen
• Glücksrad drehen
• Gameshow Prinzip – Tür, Box oder Durchgang wählen

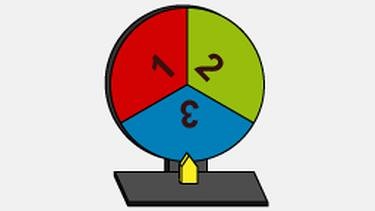
Ω = {1, 2, 3}

Beim Drehen des Glücksrades kannst du als Ergebnis also entweder die 1, die 2 oder die 3 erhalten.

Da die Flächen der jeweiligen Zahlen gleich groß sind, besitzt jedes Ergebnis die gleiche Wahrscheinlichkeit beim Drehen angezeigt zu werden.

Kein Laplace Experiment

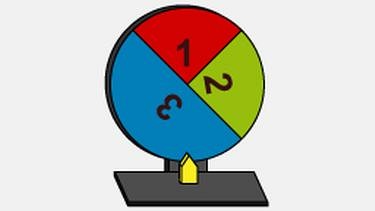
Auch bei diesem Glücksrad ergibt sich beim Drehen wieder die Ergebnismenge:

Ω = {1, 2, 3}.

Da die Fläche der Zahl 3 jedoch größer ist, als die Flächen der Zahlen 1 und 2, besitzen die drei Zahlen nicht mehr die gleiche Wahrscheinlichkeit. Die Wahrscheinlichkeit von Zahl 3 ist höher als die der Zahlen 1 und 2.

Wir werfen einen sechsseitigen Würfel und möchten verschiedene Wahrscheinlichkeiten bei dem Versuch berechnen:

• Wie groß ist die Wahrscheinlichkeit, die Zahl 3 zu Würfeln?
• Wie groß ist die Wahrscheinlichkeit, entweder eine 1 oder 4 zu Würfeln

Wir wissen, dass der Würfel sechs gleiche Seiten hat. Somit können als Ergebnis beim Würfeln die Zahlen 1, 2, 3, 4, 5 oder 6 geworfen werden. Die Anzahl der möglichen Ergebnisse beträgt somit „6“. Kommen wir nun zu den drei Teilaufgaben:

• P({3}) = 1 : 6 = 0,1666…
• P({1, 4}) = 2 : 6 = 0,33333…

Historische Bemerkungen

Statistik : „Ich würfle n mal und berechne….“ Verfahren, um empirische Daten zu gewinnen, darzustellen, zu verarbeiten, zu analysieren, ..

Wahrscheinlichkeitstheorie : „Ich sage für die Zukunft voraus….“ Bestimmung eines Maßes für den Grad der Möglichkeit des Eintreffens noch unverwirklichter Ereignisse.

Stochastik : „Mathematik des Zufalls“, Sammelbegriff für die Gebiete Statistik und Wahrscheinlichkeitstheorie

Die häufigsten Fehler beim LaPlace Experiment

Haben wir es also tatsächlich mit einem LaPlace Experiment zu tun, können alle Ergebnisse mit der gleichen Wahrscheinlichkeit folgen. Dabei spielt uns vor allen Dingen die menschliche Intuition ein Schnippchen. Wirfst du zum Beispiel eine Münze, entspricht die Menge der Ergebnisse Omega: KK, KZ, ZK, ZZ. Diese Ereignisse besitzen die gleiche Wahrscheinlichkeit.

Ist einem Spieler die Reihenfolge herzlich egal, verändert sich auch die Menge der Ergebnisse zu: KK KZ ZZ – das Ergebnis KZ trifft mit doppelter Wahrscheinlichkeit zu? Werfen wir also eine Münze 2 Mal, können wir dies noch recht schnell erkennen. Bei anderen Experimenten ist das gar nicht mehr so übersichtlich.

Vollkommen durcheinander gerät unsere Logik, wenn eine Familie mit zwei Kindern in das Münzexperiment einsteigt und damit beginnt, jeweils die Münzen zu werfen. Klar, es steht 50 zu 50, ob nun das erste oder zweite Kind beginnt die Münze zu werfen. Dabei ist aber die Wahrscheinlichkeit für Mädchen und Junge doppelt so hoch zu berechnen.

Aus diesem Grund solltest du von Anfang an genauestens nachdenken, ob die Ergebnisse mit der gleichen Wahrscheinlichkeit auftreten. Bei berechtigten Zweifeln kann ein Baumdiagramm weiterhelfen.

Fazit zum LaPlace Experiment

Im Prinzip müssen wir davon ausgehen, dass es in der Realität eigentlich keines der LaPlace Experimente gibt, da die Wirklichkeit immer von der Theorie abweicht. Wir haben es hier mit reinen Zufallsexperimenten zu tun, bei denen alle Ergebnisse mit der gleichen Wahrscheinlichkeit auftreten. So ist davon auszugehen, dass es sich bei der Münze und dem Würfel, um den Willen einer Person im Raum und um ein  LaPlace Experiment handelt.

• ← Binomialverteilung
• Varianz berechnen →

Das könnte für dich auch interessant sein

Mehrstufige zufallsexperimente, erwartungswert, binomialkoeffizient.