importance of stern gerlach experiment

• IOP Publishing
• Follow us on Facebook
• Follow us on Twitter
• Follow us on LinkedIn
• Watch us on Youtube
• Enter e-mail address
• Enter password Show
• Remember me Forgot your password?
• Access more than 20 years of online content
• Manage which e-mail newsletters you want to receive
• Read about the big breakthroughs and innovations across 13 scientific topics
• Explore the key issues and trends within the global scientific community
• Choose which e-mail newsletters you want to receive

Reset your password

Please enter the e-mail address you used to register to reset your password

Note: The verification e-mail to change your password should arrive immediately. However, in some cases it takes longer. Don't forget to check your spam folder.

If you haven't received the e-mail in 24 hours, please contact [email protected]

Registration complete

Thank you for registering with Physics World If you'd like to change your details at any time, please visit My account

• Quantum mechanics

How the Stern–Gerlach experiment made physicists believe in quantum mechanics

A century ago, the German physicists Otto Stern and Walther Gerlach carried out an experiment that gave an important credibility boost to the new-fangled notion of quantum mechanics. But as Hamish Johnston discovers, their now-famous experiment succeeded even if the physics on which it was based wasn’t quite right

Despite its counter-intuitive weirdness, quantum mechanics ranks as one of the most successful scientific theories of all time. Apart from forming the bedrock of our understanding of atoms and subatomic particles, it has spawned a host of technologies from the laser and transistor to quantum cryptography and quantum computers . But quantum mechanics wasn’t always held in such high regard.

At the start of the 20th century, when the subject was just getting off the ground, many scientists were sceptical of this new-fangled theory. Among the doubters was Otto Stern, who, along with fellow German physicist Walther Gerlach, devised a now-famous experiment to disprove the theory.

Carried out 100 years ago, the experiment involved the two physicists using beams of atoms to test a seemingly bizarre consequence of quantum mechanics known as the “space quantization of angular momentum”. As it happens, their initial interpretation of the experiment proved to be wrong. But their work spurred the development of quantum theory and today the “Stern–Gerlach experiment” is considered a classic of modern physics.

The Stern–Gerlach experiment is at the centre of the venerable conceptual puzzles of quantum mechanics – from the uncertainty principle to entanglement Bretislav Friedrich, Fritz Haber Institute, Berlin

“It’s at the centre of the venerable conceptual puzzles of quantum mechanics – from the uncertainty principle to entanglement,” says Bretislav Friedrich , a physicist from the Fritz Haber Institute in Berlin who has written extensively about the experiment and Stern and Gerlach’s lives. The experiment, he says, was greeted with “pure astonishment” in 1922 – and it still astonishes physicists today.

Quantum weirdness

Born in 1888 in the Prussian city of Sohrau (now Żory in Poland), Stern was a physical chemist by training, who did a PhD at the University of Breslau on the osmotic pressure of solutions of carbon dioxide. In 1912 he moved to the Charles-Ferdinand University in Prague, attracted by Albert Einstein, who was based there at the time. By attending Einstein’s lecturers in Prague – and later at the ETH Zurich where both moved the following year – Stern quickly became exposed to the early ideas of quantum mechanics.

These ideas included Niels Bohr’s early model of the atom, which was the centrepiece of what is now called the “old quantum theory” . Familiar today as a basic representation of an atom, the Bohr model describes an atom as a dense, positively charged nucleus orbited by negatively charged electrons.

According to classical physics, such electrons should radiate energy and spiral into the nucleus in a matter of picoseconds. As that does not happen in reality, Bohr got around this problem by restricting the electrons to specific atomic orbits, more commonly referred to as orbitals.

Orbital quantization enabled Bohr to explain a phenomenon that had puzzled physicists and chemists for decades – the fact that atoms only absorb and emit light at a discrete set of optical wavelengths. Bohr’s model initially seemed like the right idea, as it allowed him to reproduce a formula for these wavelengths that had been derived in 1888 by the Swedish physicist Johannes Rydberg . The Rydberg formula had given the wavelengths in terms of a series of integers, which we now understand to be the principal quantum numbers of the atomic orbitals.

Quantum theory: weird and wonderful

But as Bohr’s model was studied and honed by leading physicists of the day, something odd became apparent. As a consequence of orbital quantization, it transpired that the component of an electron’s orbital angular momentum along a specific direction must also be quantized. In particular, according to Bohr’s model, an electron in the lowest energy orbital should have only two values of angular momentum along any arbitrary direction. These values would point in opposite directions in space, with no intermediate values permitted.

Known as space quantization, this phenomenon was viewed as even more bizarre than orbital quantization. In fact, Stern was so sceptical of the Bohr model that he vowed to quit physics if it proved to be correct. In 1914, after Stern parted company with Einstein and joined the brand-new University of Frankfurt, a practical opportunity arose for him to put space quantization to the test. Stern realized that if an electron’s orbital angular momentum showed space quantization, then so too would the magnetic moment of an atom.

Testing for space quantization

Stern’s work was initially disrupted by the First World War, when he served in the German army on the Russian front. But on his return to Frankfurt, Stern began experiments on beams of atoms, which had become possible thanks to the invention of the mercury-diffusion vacuum pump by the German physicist Wolfgang Gaede in 1915. This device allowed researchers to create high-vacuum conditions for the first time so that atoms could travel the length of an experimental apparatus without scattering from air molecules.

In 1920 Stern was joined in Frankfurt by Gerlach, who – like Stern – had also served in the First World War. Gerlach had become involved in atomic-beam experiments through his interest in the properties of atoms in magnetic solids. In particular, Gerlach wanted to see if atoms have magnetic moments and had begun thinking about an experiment involving a beam of bismuth atoms travelling through a region with an inhomogeneous magnetic field.

If an atom has a dipole magnetic moment, Gerlach reasoned, it will experience a torque due to the magnetic field and will therefore rotate. But if the magnetic field is not uniform, the force at one end of a dipole will be stronger than the torque at the opposite end. That will lead to a net force on the atom, which will deflect as its flies through the inhomogeneous magnetic field – with the size of the deflection revealing the magnitude of the atom’s magnetic moment.

In 1921 Stern realized that such an experiment would be a great way to test for space quantization. If atoms have magnetic moments that can point in any direction (as classical physics would suggest) then the beam of atoms would broaden continuously as it passes through the inhomogeneous magnetic field. However, if the magnetic moments of the atom are space quantized – pointing in opposite directions (up and down) along the inhomogeneous field – then the beam of atoms would be split in two.

As a result, the up and down atoms would be deflected in opposite directions, providing clear evidence for space quantization. So confident was Stern of his idea that he published a paper in the journal Zeitschrift für Physik ( 7 249) that presented meticulous calculations describing how it could be done using a beam of silver atoms. Gerlach was convinced and started to build his apparatus in 1921. Stern (a theorist) and Gerlach (an experimentalist) proved an effective combination.

Experimental breakthrough

In the original version of the Stern–Gerlach experiment, the two physicists vapourized silver in an oven and allowed some atoms to escape through a hole (see box 1). They then sent the atoms through a pair of collimators, which created a beam that travelled between the two pole pieces of an electromagnet. These pieces provided a magnetic field with the required high level of inhomogeneity because one had a groove cut into it, while the other had a sharp, knife-like edge and was held above the groove.

After passing through the magnet, the beam struck a detector plate where the presence of silver could be revealed by a chemical development process similar to that used in photography. But despite its simplicity, the experiment was fiendishly difficult to undertake.

The apparatus was small – about the size of a fountain pen – and had to be kept under high vacuum using two of Gaede’s diffusion pumps. In fact, the apparatus often broke, making it difficult to achieve the long run time needed to accumulate enough silver on the detector plate to create a visible image.

1 The original set-up

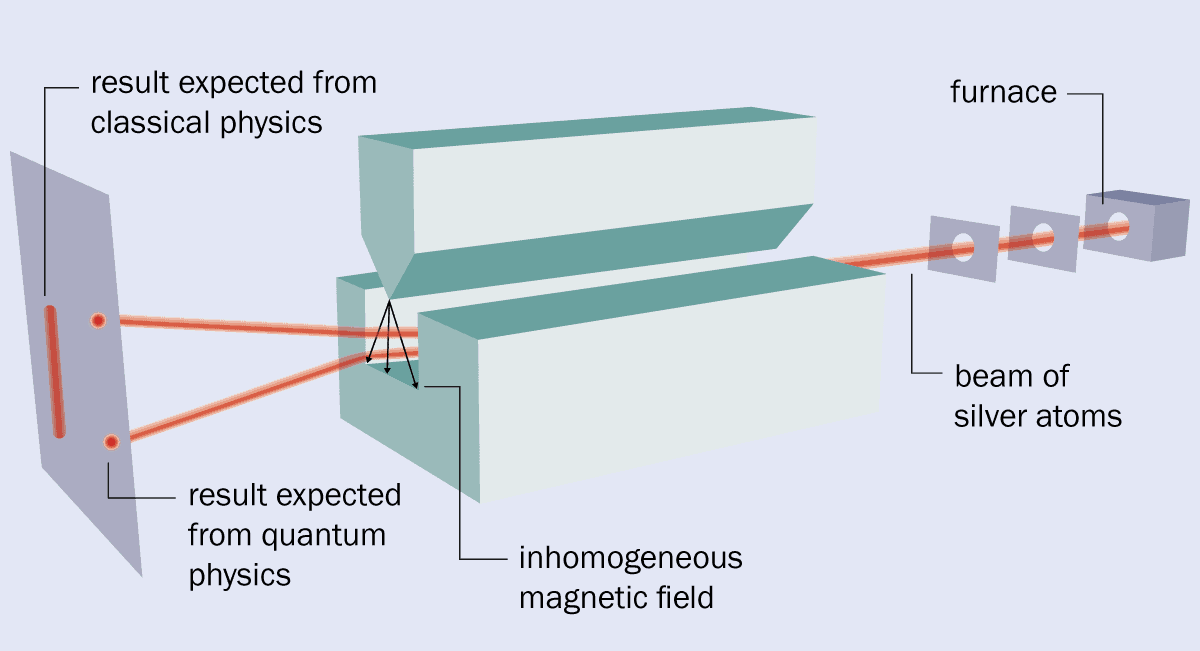
What’s more, the Stern–Gerlach experiment was expensive, made worse by the hyperinflation that was rampaging through post-war Germany. Money and donated equipment had to be secured from a range of sources including the Physikalischer Verein Frankfurt (Frankfurt Physics Society), ticket sales from popular lectures by Max Born, and donations from Einstein and Henry Goldman – an American banker and son of the co-founder of the financial firm Goldman–Sachs.

At first, Stern and Gerlach only saw their beam broadening when the inhomogeneous magnetic field was switched on. This was not the splitting predicted by quantum mechanics, but was an important achievement in its own right, being the first experimental evidence for atoms having magnetic moments. After Stern left Frankfurt in late 1921 to take up a professorship of theoretical physics at the University of Rostock, Gerlach realized that he could improve the measurement by replacing the round holes in the collimators with slits, which boosted the number of atoms in the beam.

And so, working alone one February night in 1922, Gerlach finally saw the beam splitting that had been predicted. He immediately sent a telegram to Stern saying: “Bohr is right after all”. Gerlach also created a postcard showing the split beam and sent it to Bohr, congratulating him for creating his model of the atom. Their paper presenting the results, published in December 1922 ( Zeit. Phys. 9 349) , provided the first experimental evidence for space quantization in a magnetic field – and thereby crucial evidence for quantum theory.

A new spin on things

The Stern–Gerlach experiment caused an immediate stir in the physics community, with Wolfgang Pauli, for example, quipping that  “This should convert even the non-believer Stern”. However, the explanation for the observed beam splitting using Bohr’s model was short-lived.

Other physicists, including Pauli and Paul Dirac, soon realized that the electron has an intrinsic angular momentum or spin – something that was not included Bohr’s model. What’s more, Bohr had been wrong to predict that the ground state of the silver atom has orbital angular momentum; it does not.

Today we know that the splitting that Stern and Gerlach saw in their experiment is actually caused by the spin of silver’s unpaired electron. Indeed, the Stern–Gerlach experiment is now interpreted as evidence of electron spin, rather than as proof of space quantization.

As so often in physics, even supposedly “wrong” results can still lead to progress. What’s more, the work opened the door to a huge variety of other findings, including showing the momentum transfer that occurs if an atom emits or absorbs a photon.

Stern went on to carry out the world’s first matter-wave experiments with atoms when he scattered beams of atoms off the surfaces of crystals, which confirmed the principle of wave-particle duality. Later, in 1933, he measured the magnetic dipole moment of the proton using a set-up similar to the Stern–Gerlach experiment. He found it to be larger than expected, which suggested that the proton is not a point-like particle – as had been assumed at the time – but rather has internal structure. This discovery led Stern to win the Nobel Prize for Physics in 1943 .

By that time, Stern – who was Jewish by birth – was based at the Carnegie Institute of Technology in Pittsburgh in the US, having fled Germany in 1933 as Nazi repression of the Jews intensified. While at Carnegie, he extended his work on the magnetic dipole moment of the proton to its heavier cousin, the deuteron. Stern’s lab in Pittsburgh also confirmed Maxwell–Boltzmann velocity distribution of particles in an ideal gas. He died in the US in 1969.

As for Gerlach, he went on to measure the magnetic moment of atomic bismuth and several other metals using the atomic beam technique. He also did experiments on the radiation pressure of light and continued his interest in magnetism and condensed-matter physics. His career later took him to the universities of Tübingen and Munich. Despite being nominated 31 times between 1924 and 1944, Gerlach missed out on a Nobel prize.

[The pair benefitted from] Stern’s ideas on the one hand and Gerlach’s realism and skills in the lab as well as a – sometimes stubborn – determination to make things work Bretislav Friedrich, Fritz Haber Institute, Berlin

Like Stern, Gerlach was impacted by Nazism – but in a very different way. Although he never joined the Nazi party and rejected the idea of “Jewish science” , Gerlach headed Germany’s nuclear research programme in the final years of the Second World War. He ended up being interned by the Allied Forces at Farm Hall in England along with nine other German physicists suspected of being involved in Germany’s nuclear weapons programme including Max von Laue and Werner Heisenberg .

The quantum heretics

After the war, Gerlach returned to academic research, spending the bulk of his career back at Munich where he played important roles in rebuilding German science. In 1957, he, von Laue and Heisenberg were part of a group of 18 leading German physicists who signed the Göttingen Manifesto , which rejected a proposal by the then chancellor Konrad Adenauer to arm Germany with nuclear weapons. Gerlach died aged 90 in 1979.

Lasting impact

Apart from shaping the course of modern science, the Stern–Gerlach experiment has also had a huge practical impact. Indeed, Stern is widely viewed as one of the founders of experimental atomic, molecular and nuclear physics , having shown how molecular beams can be used to quantitatively study matter without resorting to spectroscopy. “Sorting states via space quantization is ubiquitous,” says Friedrich, with nuclear magnetic resonance and magnetic-resonance imaging being the most direct descendants of the classic experiment.

Friedrich also credits the Stern–Gerlach experiment for introducing principles that influenced other areas of science, such as the development of the maser and laser. And although Gerlach missed out on a Nobel prize, Friedrich says his recruitment by Stern was a “stroke of luck” for atomic physics, with the pair having exceptional complementary talents. “[They benefitted from] Stern’s ideas on the one hand and Gerlach’s realism and skills in the lab as well as a – sometimes stubborn – determination to make things work.”

• For more on the Stern–Gerlach experiment, see Molecular Beams in Physics and Chemistry: From Otto Stern’s Pioneering Exploits to Present-Day Feats edited by Bretislav Friedrich and Horst Schmidt-Böcking (2022 Springer).

Want to read more?

Note: The verification e-mail to complete your account registration should arrive immediately. However, in some cases it takes longer. Don't forget to check your spam folder.

If you haven't received the e-mail in 24 hours, please contact [email protected] .

• E-mail Address

Free Peer Review Excellence online course

Get peer review confident with our free, certified, course.

• Diversity and inclusion

The joy of connecting quantum black dots

Climate tipping points: retreating from the brink and accelerating positive change, discover more from physics world.

Ask me anything: Nadya Mason ‘I find myself looking at everything as systems of equations’

• Quantum computing

Two advances in quantum error correction share the Physics World 2024 Breakthrough of the Year

Mikhail Lukin and Dolev Bluvstein explain how they used trapped atoms to create 48 logical qubits

Related jobs, physics faculty positions at westlake university, w3 professorship for collective phenomena in quantum physics, recruitment of overseas high-level talent, related events.

• Quantum | Conference Quantum.Tech Qatar 2025: Commercial Applications of Quantum Computing, Communications and Sensing 13—15 January 2025 | Doha, Qatar
• Quantum | Workshop Machine Learning for Quantum Matter 24—28 February 2025 | Dresden, Germany
• Quantum | School Boulder Summer School: Dynamics of Strongly Correlated Electrons 30 June — 25 July 2025 | Boulder, US

• Table of Contents
• Random Entry
• Chronological
• Editorial Information
• About the SEP
• Editorial Board
• How to Cite the SEP
• Special Characters
• Advanced Tools
• Support the SEP
• PDFs for SEP Friends
• Make a Donation
• SEPIA for Libraries
• Back to Entry
• Entry Contents
• Entry Bibliography
• Academic Tools
• Friends PDF Preview
• Author and Citation Info
• Back to Top

Supplement to Experiment in Physics

Appendix 5: right experiment, wrong theory: the stern-gerlach experiment.

From the time of Ampere onward, molecular currents were regarded as giving rise to magnetic moments. In the nuclear model of the atom the electron orbits the nucleus. This circular current results in a magnetic moment. The atom behaves as if it were a tiny magnet. In the Stern-Gerlach experiment a beam of silver atoms passed through an inhomogeneous magnetic field (Figure 12). In Larmor’s classical theory there was no preferential direction for the direction of the magnetic moment and so one predicted that the beam of silver atoms would show a maximum in the center of the beam. In Sommerfeld’s quantum theory an atom in a state with angular momentum equal to one \((L = 1)\) would have a magnetic moment with two components relative to the direction of the magnetic field, \(\pm eh/4m_e\). (Bohr had argued that only two spatial components were allowed). In an inhomogeneous magnetic field, \(\bH\), the force on the magnetic moment \(\mu\) will be \(\mu_z x\) (Gradient of the magnetic field in the \(z\) direction), where \(\mu_z = \pm eh/4m_e\), where \(e\) is the charge of the electron, \(m_e\) is its mass, \(h\) is Planck’s constant, and \(z\) is the field direction. Thus, depending on the orientation of the magnetic moment relative to the magnetic field there will be either an attractive or repulsive force and the beam will split into two components, exhibiting spatial quantization. There will be a minimum at the center of the beam. “According to quantum theory \(\mu_z\) can only be \(\pm(e/2m_e)(h/2\pi)\). In this case the spot on the receiving plate will therefore be split into two, each of them having the same size but half the intensity of the original spot” (Stern 1921, p. 252, JM) This difference in prediction between the Larmor and Sommerfeld theories was what Stern and Gerlach planned to use to distinguish between the two theories. Stern remarked that “the experiment, if it can be carried out, (will result) in a clear-cut decision between the quantum-theoretical and the classical view” (Stern 1921, FW).

Figure 12. Sketch of the Stern-Gerlach experimental apparatus. The result expected for atoms in an \(L = 1\) state (three components) is shown. From Weinert (1995).

Sommerfeld’s theory also acted as an enabling theory for the experiment. It provided an estimate of the size of the magnetic moment of the atoms so that Stern could begin calculations to see if the experiment was feasible. Stern calculated, for example, that a magnetic field gradient of 10 4 Gauss per centimeter would be sufficient to produce deflections that would give detectable separations of the beam components. He asked Gerlach if he could produce such a gradient. Gerlach responded affirmatively, and said he could do even better. The experiment seemed feasible. A sketch of the apparatus is shown in Figure 12. The silver atoms pass through the inhomogeneous magnetic field. If the beam is spatially quantized, as Sommerfeld predicted, two spots should be observed on the screen. (The sketch shows the beam splitting into three components, which would be expected in modern quantum theory for an atom with angular momentum equal to one). I note that Sommerfeld’s theory was incorrect, illustrating the point that an enabling theory need not be correct to be useful.

Figure 13. The experimental result of the Stern-Gerlach experiment. The beam has split into two components. From Gerlach and Stern (1922a).

A preliminary result reported by Stern and Gerlach did not show splitting of the beam into components. It did, however, show a broadened beam spot. They concluded that although they had not demonstrated spatial quantization, they had provided “evidence that the silver atom possesses a magnetic moment.” Stern and Gerlach made improvements in the apparatus, particularly in replacing a round beam slit by a rectangular one that gave a much higher intensity. The results are shown in Figure 13 (Gerlach and Stern 1922a). There is an intensity minimum in the center of the pattern, and the separation of the beam into two components is clearly seen. This result seemed to confirm Sommerfeld’s quantum-theoretical prediction of spatial quantization. Pauli, a notoriously skeptical physicist, remarked, “Hopefully now even the incredulous Stern will be convinced about directional quantization” (in a letter from Pauli to Gerlach 17 February 1922). Pauli’s view was shared by the physics community. Nevertheless the Stern-Gerlach result posed a problem for the Bohr-Sommerfeld theory of the atom. Stern and Gerlach had assumed that the silver atoms were in an angular momentum state with angular momentum equal to one \((L = 1)\). In fact, the atoms are in an \(L = 0\) state, for which no splitting of the beam would be expected in either the classical or the quantum theory. Stern and Gerlach had not considered this possibility. Had they done so they might not have done the experiment. The later, or new, quantum theory developed by Heisenberg, Schrodinger, and others, predicted that for an \(L = 1\) state the beam should split into three components as shown in Figure 12. The magnetic moment of the atom would be either 0 or \(\pm eh/(4\pi x m)\). Thus, if the silver atoms were in an \(L = 1\) state as Stern and Gerlach had assumed, their result, showing two beam components, also posed a problem for the new quantum theory. This was solved when Uhlenbeck and Goudsmit (1925, 1926) proposed that the electron had an intrinsic angular momentum or spin equal to \(h/4\pi\). This is analogous to the earth having orbital angular momentum about the sun and also an intrinsic angular momentum due to its rotation on its own axis. In an atom the electron will have a total angular momentum \(\bJ = \bL + \bS\), where \(\bL\) is the orbital angular momentum and \(\bS\) is the spin of the electron. For silver atoms in an \(L = 0\) state the electron would have only its spin angular momentum and one would expect the beam to split into two components. Goudsmit and Uhlenbeck suggested the idea of electron spin to explain features in atomic spectra such as the anomalous Zeeman effect, the splitting of spectral lines in a magnetic field into more components than could be accommodated by the Bohr-Sommerfeld theory of the atom. Although the Stern-Gerlach results were known, and would certainly have provided strong support for the idea of electron spin, Goudsmit and Uhlenbeck made no mention of the result.

The Stern-Gerlach experiment was initially regarded as a crucial test between the classical theory of the atom and the Bohr-Sommerfeld theory. In a sense it was, because it showed clearly that spatial quantization existed, a phenomenon that could be accommodated only within a quantum mechanical theory. It decided between the two classes of theories, the classical and the quantum mechanical. With respect to the particular quantum theory of Bohr and Sommerfeld, however, it wasn’t crucial, although it was regarded as such at the time, because that theory predicted no splitting for a beam of silver atoms in the ground state \((L = 0)\). The theory had been wrongly applied. The two-component result was also problematic for the new quantum theory, which also predicts no splitting for an angular momentum zero state and three components for an \(L = 1\) state. Only after the suggestion of electron spin did the Stern-Gerlach result confirm the new theory.

Although the interpretation of the experimental result was incorrect for a time, the result itself remained quite robust through the theory change from the old to the new quantum theory. It is important to remember that experimental results do not change when accepted theory changes, although certainly, as we have seen, their interpretation may change. Gerlach and Stern emphasized this point themselves.

Apart from any theory, it can be stated, as a pure result of the experiment, and as far as the exactitude of our experiments allows us to say so, that silver atoms in a magnetic field have only two discrete values of the component of the magnetic moment in the direction of the field strength; both have the same absolute value with each half of the atoms having a positive and a negative sign respectively (Gerlach and Stern 1924, pp. 690–691, FW)

Experimental results, as well as experiments, also have a life of their own, independent of theory.

Return to Experiment in Physics

Copyright © 2023 by Allan Franklin < allan . franklin @ colorado . edu > Slobodan Perovic < sperovic @ f . bg . ac . rs >

• Accessibility

Support SEP

Mirror sites.

View this site from another server:

• Info about mirror sites

The Stanford Encyclopedia of Philosophy is copyright © 2023 by The Metaphysics Research Lab , Department of Philosophy, Stanford University

Library of Congress Catalog Data: ISSN 1095-5054

• Chapter 1: Stern-Gerlach Experiments
• View page source

Chapter 1: Stern-Gerlach Experiments 

The hardest part of learning something new is not embracing new ideas, but letting go of old ones. ― Todd Rose, The End of Average: How We Succeed in a World That Values Sameness

The first steps we take in our exploration of the quantum mechanical world bring us at the doorstep of a key experiment, whose outcome cannot be explained by classical physics alone. The experiment was devised by Stern and Gerlach to study the intrinsic angular momentum of electrons. Stern-Gerlach (SG) experiments demonstrate that particles ( i.e. , electrons) do not behave classically.

First, the experiments indicate that the particles possess an angular momentum that is not classical (a classical momentum is called an orbital angular momentum arising from a particle that rotates, for example, as we will study in Chapter 10: Bound states of central potential ). Judging from the experimental results, the spin angular momentum seems to present some properties of the classical angular momentum but also displays a drastically distinct behavior. For instance, its projection on a given axis takes discrete values (in our example, two of them only, as demonstrated in the first SG experiment).

What are the Stern-Gerlach (SG) experiments? 

This apparatus allows for the measurement of the magnetic moment of a particle. The interaction between the magnetic moment and the external magnetic field provides a net force on the particle. It follows the deflection of the particle can be used to determine the magnetic moment of the particle. Important note: in order to generate a force, the magnetic field must be non-uniform as the force goes as: It is essential to remember that in the SG experiments, the particle does not have a classical angular momentum so any deflection must be due to something else , which is not classical. Through a series of SG experiments, one realizes that we must define a new framework, beyond classical physics, to try to account for those measurements.

Learning Material 

Copy of slides , screencast .

Key Learning Points 

The probability (a real number between 0 and 1) is given by the square modulus of the probability amplitude:

Those coefficients are complex numbers and are given by projections on the basis vectors:

Test your knowledge 

because of the electric field generated by the magnet.

because of the presence of a uniform magnetic field and the fact the electrons have a magnetic moment.

because of the presence of a non-uniform magnetic field and the fact the electrons have a magnetic moment.

None of the other answers is correct.

Electrons behave classically for the most part.

Electrons have an intrinsic magnetic moment even when their (classical) orbital momentum is zero.

An electron seems to have a quantum mechanical angular momentum, distinct from its orbital angular momentum and that momentum can take any continuous value between a maximum and a minimum.

It is a mathematical or abstract object that describes a given system. All of the information about the system is included in it, though one does not necessarily have easy access to that information.

It is a mathematical or abstract object that describes a given system. It includes some information about the system: the information one has already obtained with a measurement.

A ket vector is just a wave-function.

It is a mathematical object that has very little use outside of IQM.

It is a mathematical object that includes the exact same information on the system as the corresponding ket does. However, it “lives” in a different space and it allows IQM students to perform dot products.

Smaller plus z vertical bar plus x larger.

Find the answer keys on this page: Answers to selected test your knowledge questions . Don’t cheat! Try solving the problems on your own first!

Homework Assignment 

Solve the following problems from the textbook: 1.3; 1.4; 1.5; 1.8, 1.11, 1.15

Physicus Minimus

Über kleine Teilchen und kleine Physiker:innen

The Stern-Gerlach Experiment – A history of stubbornness

Even scientists are only human. That’s why success stories often read like a comic book: great heroes fighting for the good of humanity. From another perspective, however, it sometimes seems more like the nagging of old white men arguing over who is right. We have already seen a few examples of this: Boltzmann and Planck fighting over entropy , Thomson and Rutherford decoding the atom , Newton and the rest of the world racking their brains over the nature of light . And the Stern-Gerlach experiment, which celebrated its hundredth anniversary this month and which is a milestone of quantum physics, was ultimately the invention of a scientist who desperately wanted to be right.

The Stern-Gerlach experiment was carried out by Otto Stern and Walter Gerlach in Frankfurt on the night of 7 to 8 February 1922. Otto Stern was a Jewish-born theoretical physicist and the brains behind the experiment, who – like so many scientists – left Germany in 1933. Walther Gerlach was an experimental physicist, the “maker” of the experiment, and was… well, if not a Nazi, at least useful to the Nazi regime as “Reichsmarschall für Kernphysik” ( Imperial Marshall of Nuclear Physics ). This probably contributed to the fact that the Otto Stern Centre at Goethe University Frankfurt only honours one of the two scientists. But perhaps it was also because only Stern was awarded the Nobel Prize for physics in 1943 – without Gerlach.

We already see the first rudiments of human drama here. But the announced squabble was not about dissents between Stern and Gerlach. At the beginning of the famous Stern-Gerlach experiment stood Stern, who thought Bohr’s and Sommerfeld’s atomic model was nonsense .

Bohr’s Atomic Model

It is 1913 and amazingly little is known about the structure of atoms – the basic building blocks of matter (you can find an overview of earlier atomic models here ). Only a few years earlier, Ernest Rutherford had substantiated his atomic model with his historic Rutherford scattering experiment : the atom is composed of a positively charged nucleus and negatively charged electrons buzzing around it.

Anyone who knows a little about classical electrodynamics knows that this is utter nonsense! Positive and negative charges attract each other! An atom constructed in this way would be highly unstable . The electron would have to circle into the nucleus and emit radiation with decreasing frequency. But that doesn’t fit, because we already knew that atoms only emit or absorb light at very specific frequencies .

Niels Bohr tackled this problem in a very whimsical way. He set up three postulates that are the foundation for his new atomic model. Postulates are bold assertions that “remain to be proven”. Bohr’s most important (though not explicitly stated) assumption: screw classical mechanics and electrodynamics! I’m doing my thing here! Let’s take a closer look at these three postulates.

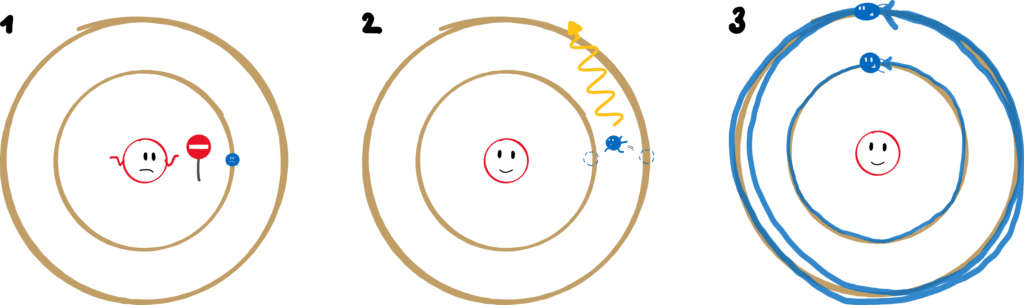
1. An electron can only move along certain orbits. On these, however, it moves radiation-free.

Only certain orbits are allowed? That contradicts classical mechanics: In principle, planets can move in any (elliptical) orbit around the sun. Electrons are only allowed very specific ones – the space in between is taboo. And they move radiation-free in these orbits? We’ve already been through that, it contradicts classical electrodynamics!

2. An electron can jump from one orbit to another (called quantum leap). In doing that, it must absorb or release exactly the right amount of energy.

Okay, if you accept postulate 1, postulate 2 kind of makes sense. If there are only certain, permitted paths, then the electron must hop from one to the other. But the fact that it only absorbs or emits energy in this process – and that in fixed portion sizes – also contradicts electrodynamics. Imagine you could only have 1 A(mpere) of current or 2 A, but not 1.1 A. Absurd.

3. The angular momentum of the electron on the orbit is an integer multiple of Planck’s constant.

That sounds a bit technical, but stay with me! The angular momentum describes, casually speaking, with how much “oomph” something turns. If an electron (metaphorically speaking) flits around the lowest orbit exactly once in a certain amount of time, then it takes exactly twice as long to go around the next higher orbit once. That this minimum angular momentum corresponds exactly to Planck’s constant is very neat and was actually only a guess by Bohr. Or to put it another way: it was precisely this value that made it possible to explain experimental observations with the help of Bohr’s atomic model. As daring as Bohr’s atomic model sounds, it was able to explain many phenomena and make concrete predictions .

The Bohr-Sommerfeld atomic model

The theoretical physicist Arnold Sommerfeld refined Bohr’s atomic model in 1916. Instead of circular orbits, he assumed elliptical orbits, as already known from the solar system. He also introduced three quantum numbers (not just one, like Bohr). Quantum numbers are integers (0, 1, 2, …, -1, -2, …) and the fundament of quantisation : physical quantities no longer lie anywhere on a number ray, but only at these integer steps.

Sommerfeld’s three quantum numbers quantise the energy, the angular momentum and the orientation of the elliptical orbit. Let me repeat that: the ORIENTATION of the orbits! There is not only a restriction on which orbits an electron may take (as Bohr already claimed), but also on how they may be oriented in space . Imagine that on a chairoplane, the seats could only point vertically downwards, upwards, or 90° to the side, but not in between! This phenomenon is called directional quantisation and could explain the behaviour of atoms in magnetic fields.

As a side note: If you look at it from a modern point of view, it is extremely fascinating how well these gentlemen have guessed . Because if you calculate the hydrogen atom once with proper quantum mechanics, you get (almost) the same quantum numbers. But wait, this was not the first lucky guess we will see today.

Stern is not happy

Otto Stern took great offence at this atomic model. Because of the violation of mechanics and electrodynamics, which have existed for centuries? No. Because of the directional quantisation of the electron orbits . He wanted to put an end to this nonsense and come up with an experiment that disproved directional quantisation.

No sooner said than done. He needed comrades-in-arms: Walther Gerlach, who was fit in experimenting, but also Max Born and the mechanic Adolf Schmidt. And they needed a lot of donations to be able to set up the experiment, which came from Albert Einstein and various companies, among others. In February 1922, everything was ready to go.

Mini-magnets in a magnetic field

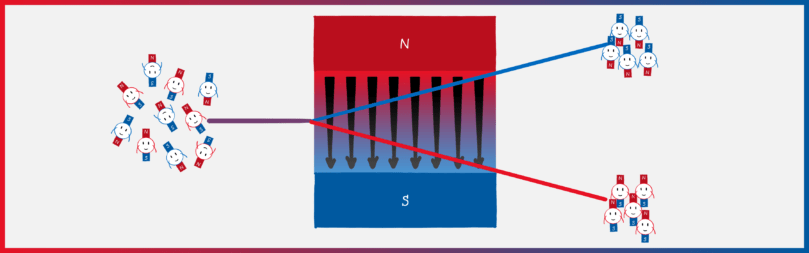
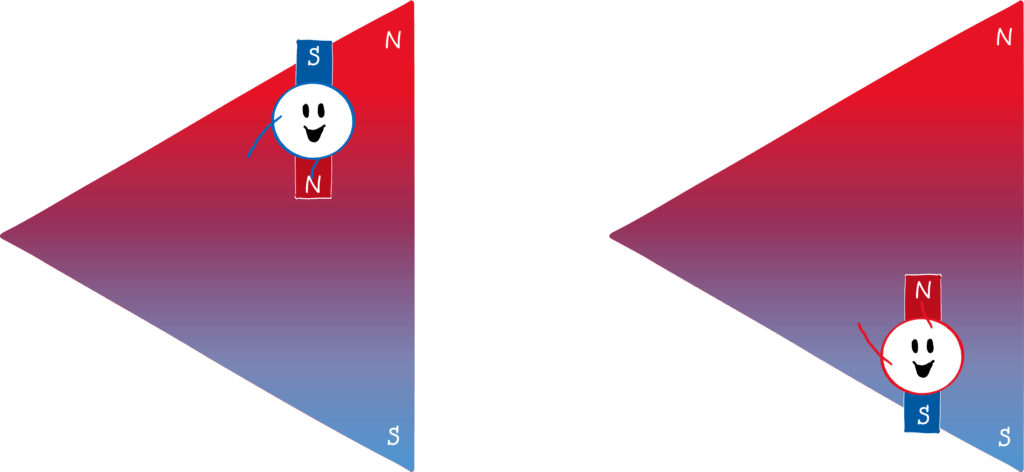
To prove (or disprove) the directional quantization, Stern and Gerlach used a well-known law of electrodynamics. It refers to the behaviour of magnetic dipoles – sort of elementary mini-magnets – in a magnetic field. The principle of a compass is that the needle (a mini-magnet) aligns itself in an external magnetic field (the earth’s magnetic field). However, the needle only rotates: if you were to build the compass on a small cart, it would not drive to the North Pole. However, this is different in an inhomogeneous, i.e. a non-uniform, magnetic field. If the magnetic field at the Earth’s north pole, for example, were much stronger than at the south pole (for example, if the Earth were not a sphere but an ice cream cone with the tip pointing upwards), the little compass cart would travel to the north pole !

Why is that? Let’s draw the north pole red and the south pole blue (picture below). Since the north pole is stronger, the upper part of the magnetic field is “redder” than the lower part is blue. If a mini-magnet (i.e. a magnetic dipole) flits through this field and its south pole points upwards (left panel), it will be deflected upwards. This is because the north and south poles of magnets attract each other . Because the magnetic field is stronger at the top than at the bottom, the red part of the field attracts the blue part of the magnet more strongly than the blue part of the field attracts the red part of the magnet. The reverse is true if the north pole of the mini-magnet points upwards (right panel). Then the red part of the field repels the red part of the magnet more strongly than the blue part of the field repels the blue part of the magnet.

The Stern-Gerlach experiment

The key of the Stern-Gerlach experiment is that atoms behave like mini-magnets . Classically , one would expect that the mini-magnets in the atom can point in any direction. If you shoot atoms through an inhomogeneous magnetic field, you should see a smeared stripe on the opposite side.

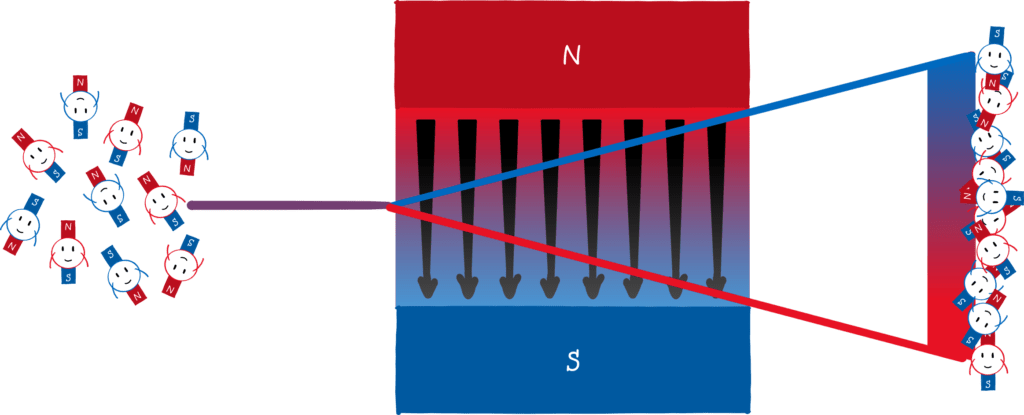
That’s exactly what Stern and Gerlach did in their experiment with silver atoms and what came out? Drum roll! Two points! Stern was so pleased that he almost forgot that he was originally against directional quantization. He wrote an excited telegram to Gerlach with the message “ Bohr is right!”. Stern is an exemplary loser. He wanted to refute Bohr and in the end, he substantiated his atomic model.

Appearances are deceptive

However, one small detail is still not right. It was later found out that the outermost electron of silver had an angular momentum of zero. You cannot “quantise” an angular momentum of zero – it is always zero. Stern and Gerlach originally assumed that the angular momentum was 1, so it could have pointed upwards (1), downwards (-1) or towards the centre (0). But the fact that two, and not the expected three, points were seen in the experiment apparently didn’t really bother anyone. But with an angular momentum of 0, there are no mini-magnets. So one should not observe any deflection of the atoms at all . It took three years to resolve this puzzle.