case study cbse class 10 maths

Andhra Pradesh
Chhattisgarh
West Bengal
Madhya Pradesh
Maharashtra
Jammu & Kashmir
NCERT Books 2022-23
NCERT Solutions
NCERT Notes
NCERT Exemplar Books
NCERT Exemplar Solution
States UT Book
School Kits & Lab Manual
NCERT Books 2021-22
NCERT Books 2020-21
NCERT Book 2019-2020
NCERT Book 2015-2016
RD Sharma Solution
TS Grewal Solution
TR Jain Solution
Selina Solution
Frank Solution
Lakhmir Singh and Manjit Kaur Solution
I.E.Irodov solutions
ICSE - Goyal Brothers Park
ICSE - Dorothy M. Noronhe
Micheal Vaz Solution
S.S. Krotov Solution
Evergreen Science
KC Sinha Solution
ICSE - ISC Jayanti Sengupta, Oxford
ICSE Focus on History
ICSE GeoGraphy Voyage
ICSE Hindi Solution
ICSE Treasure Trove Solution
Thomas & Finney Solution
SL Loney Solution
SB Mathur Solution
P Bahadur Solution
Narendra Awasthi Solution
MS Chauhan Solution
LA Sena Solution
Integral Calculus Amit Agarwal Solution
IA Maron Solution
Hall & Knight Solution
Errorless Solution
Pradeep's KL Gogia Solution
OP Tandon Solutions
Sample Papers
Previous Year Question Paper
Important Question
Value Based Questions
CBSE Syllabus
CBSE MCQs PDF
Assertion & Reason
New Revision Notes
Revision Notes
Question Bank
Marks Wise Question
Toppers Answer Sheets
Exam Paper Aalysis
Concept Map
CBSE Text Book
Additional Practice Questions
Vocational Book
CBSE - Concept
KVS NCERT CBSE Worksheets
Formula Class Wise
Formula Chapter Wise
Toppers Notes
Most Repeated Question
Diagram Based Question
Study Planner
Competency Based Questions
JEE Previous Year Paper
JEE Mock Test
JEE Crash Course
JEE Sample Papers
JEE Toppers Notes
JEE Formula
JEE Important Question
JEE Mind Map
JEE Integer-Numerical Type Question
JEE Study Planner
Important Info
SRM-JEEE Previous Year Paper
SRM-JEEE Mock Test
VITEEE Previous Year Paper
VITEEE Mock Test
BITSAT Previous Year Paper
BITSAT Mock Test
Manipal Previous Year Paper
Manipal Engineering Mock Test
AP EAMCET Previous Year Paper
AP EAMCET Mock Test
COMEDK Previous Year Paper
COMEDK Mock Test
GUJCET Previous Year Paper
GUJCET Mock Test
KCET Previous Year Paper
KCET Mock Test
KEAM Previous Year Paper
KEAM Mock Test
MHT CET Previous Year Paper
MHT CET Mock Test
TS EAMCET Previous Year Paper
TS EAMCET Mock Test
WBJEE Previous Year Paper
WBJEE Mock Test
AMU Previous Year Paper
AMU Mock Test
CUSAT Previous Year Paper
CUSAT Mock Test
AEEE Previous Year Paper
AEEE Mock Test
UPSEE Previous Year Paper
UPSEE Mock Test
CGPET Previous Year Paper
BCECE Previous Year Paper
JCECE Previous Year Paper
LPU Mock Test
Crash Course
Previous Year Paper
NCERT Based Short Notes
NCERT Based Tests
NEET Sample Paper
NEET Toppers Notes
NEET Formula
NEET Important Question
NEET Assertion Reason Question
NEET Study Planner
Previous Year Papers
Quantitative Aptitude
Numerical Aptitude Data Interpretation
General Knowledge
Mathematics
Agriculture
Accountancy
Business Studies
Political science
Enviromental Studies
Mass Media Communication
Teaching Aptitude
Verbal Ability & Reading Comprehension
Logical Reasoning & Data Interpretation
CAT Mock Test
CAT Important Question
CAT Vocabulary
CAT English Grammar
MBA General Knowledge
CAT Mind Map
CAT Study Planner
CMAT Mock Test
SRCC GBO Mock Test
SRCC GBO PYQs
XAT Mock Test
SNAP Mock Test
IIFT Mock Test
MAT Mock Test
CUET PG Mock Test
CUET PG PYQs
MAH CET Mock Test
MAH CET PYQs
NAVODAYA VIDYALAYA
SAINIK SCHOOL (AISSEE)
Mechanical Engineering
Electrical Engineering
Electronics & Communication Engineering
Civil Engineering
Computer Science Engineering
CBSE Board News
Scholarship Olympiad
School Admissions
Entrance Exams
All Board Updates
Miscellaneous
State Wise Books
Engineering Exam

Case Study Class 10 Maths Questions and Answers (Download PDF)

Free pdf download.

SHARING IS CARING If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

Case Study Class 10 Maths

If you are looking for the CBSE Case Study class 10 Maths in PDF, then you are in the right place. CBSE 10th Class Case Study for the Maths Subject is available here on this website. These Case studies can help the students to solve the different types of questions that are based on the case study or passage.

CBSE Board will be asking case study questions based on Maths subjects in the upcoming board exams. Thus, it becomes an essential resource to study.

The Case Study Class 10 Maths Questions cover a wide range of chapters from the subject. Students willing to score good marks in their board exams can use it to practice questions during the exam preparation. The questions are highly interactive and it allows students to use their thoughts and skills to solve the given Case study questions.

Download Class 10 Maths Case Study Questions and Answers PDF (Passage Based)

Download links of class 10 Maths Case Study questions and answers pdf is given on this website. Students can download them for free of cost because it is going to help them to practice a variety of questions from the exam perspective.

Case Study questions class 10 Maths include all chapters wise questions. A few passages are given in the case study PDF of Maths. Students can download them to read and solve the relevant questions that are given in the passage.

Students are advised to access Case Study questions class 10 Maths CBSE chapter wise PDF and learn how to easily solve questions. For gaining the basic knowledge students can refer to the NCERT Class 10th Textbooks. After gaining the basic information students can easily solve the Case Study class 10 Maths questions.

Case Study Questions Class 10 Maths Chapter 1 Real Numbers

Case Study Questions Class 10 Maths Chapter 2 Polynomials

Case Study Questions Class 10 Maths Chapter 3 Pair of Equations in Two Variables

Case Study Questions Class 10 Maths Chapter 4 Quadratic Equations

Case Study Questions Class 10 Maths Chapter 5 Arithmetic Progressions

Case Study Questions Class 10 Maths Chapter 6 Triangles

Case Study Questions Class 10 Maths Chapter 7 Coordinate Geometry

Case Study Questions Class 10 Maths Chapter 8. Introduction to Trigonometry

Case Study Questions Class 10 Maths Chapter 9 Some Applications of Trigonometry

Case Study Questions Class 10 Maths Chapter 10 Circles

Case Study Questions Class 10 Maths Chapter 12 Areas Related to Circles

Case Study Questions Class 10 Maths Chapter 13 Surface Areas & Volumes

Case Study Questions Class 10 Maths Chapter 14 Statistics

Case Study Questions Class 10 Maths Chapter 15 Probability

How to Solve Case Study Based Questions Class 10 Maths?

In order to solve the Case Study Based Questions Class 10 Maths students are needed to observe or analyse the given information or data. Students willing to solve Case Study Based Questions are required to read the passage carefully and then solve them.

While solving the class 10 Maths Case Study questions, the ideal way is to highlight the key information or given data. Because, later it will ease them to write the final answers.

Case Study class 10 Maths consists of 4 to 5 questions that should be answered in MCQ manner. While answering the MCQs of Case Study, students are required to read the paragraph as they can get some clue in between related to the topics discussed.

Also, before solving the Case study type questions it is ideal to use the CBSE Syllabus to brush up the previous learnings.

Features Of Class 10 Maths Case Study Questions And Answers Pdf

Students referring to the Class 10 Maths Case Study Questions And Answers Pdf from Selfstudys will find these features:-

Accurate answers of all the Case-based questions given in the PDF.
Case Study class 10 Maths solutions are prepared by subject experts referring to the CBSE Syllabus of class 10.
Free to download in Portable Document Format (PDF) so that students can study without having access to the internet.

Benefits of Using CBSE Class 10 Maths Case Study Questions and Answers

Since, CBSE Class 10 Maths Case Study Questions and Answers are prepared by our maths experts referring to the CBSE Class 10 Syllabus, it provided benefits in various way:-

Case study class 10 maths helps in exam preparation since, CBSE Class 10 Question Papers contain case-based questions.
It allows students to utilise their learning to solve real life problems.
Solving case study questions class 10 maths helps students in developing their observation skills.
Those students who solve Case Study Class 10 Maths on a regular basis become extremely good at answering normal formula based maths questions.
By using class 10 Maths Case Study questions and answers pdf, students focus more on Selfstudys instead of wasting their valuable time.
With the help of given solutions students learn to solve all Case Study questions class 10 Maths CBSE chapter wise pdf regardless of its difficulty level.

Manipal MET 2024 Application (Released) (All Pages)

NCERT Solutions for Class 12 Maths
NCERT Solutions for Class 10 Maths
CBSE Syllabus 2023-24
Social Media Channels
Login Customize Your Notification Preferences

Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Class 10 Maths Chapter 1 - Real Numbers (Published by CBSE)

Cbse class 10 maths cased study question bank for chapter 1 - real numbers is available here. this question bank is very useful to prepare for the class 10 maths exam 2021-2022..

The Central Board of Secondary Education has introduced the case study questions in class 10 exam pattern 2021-2022. The CBSE Class 10 questions papers of Board Exam 2022 will have questions based on case study. Therefore, students should get familiarised with these questions to do well in their board exam.

We have provided here case study questions for Class 10 Maths Chapter 1 - Real Numbers. These questions have been published by the CBSE board itself. Students must solve all these questions at the same time they finish with the chapter - Real numbers.

Case Study Questions for Class 10 Maths Chapter 1 - Real Numbers

To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section B of grade X. There are 32 students in section A and 36 students in section B.

1. What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?

Answer: c) 288

2. If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32 , 36) is

Answer: b) 4

3. 36 can be expressed as a product of its primes as

a) 2 2 × 3 2

b) 2 1 × 3 3

c) 2 3 × 3 1

d) 2 0 × 3 0

Answer: a) 2 2 × 3 2

4. 7 × 11 × 13 × 15 + 15 is a

a) Prime number

b) Composite number

c) Neither prime nor composite

d) None of the above

Answer: b) Composite number

5. If p and q are positive integers such that p = ab 2 and q= a 2 b, where a , b are prime numbers, then the LCM (p, q) is

Answer: b) a 2 b 2

CASE STUDY 2:

A seminar is being conducted by an Educational Organisation, where the participants will be educators of different subjects. The number of participants in Hindi, English and Mathematics are 60, 84 and 108 respectively.

1. In each room the same number of participants are to be seated and all of them being in the same subject, hence maximum number participants that can accommodated in each room are

Answer: b) 12

2. What is the minimum number of rooms required during the event?

Answer: d) 21

3. The LCM of 60, 84 and 108 is

Answer: a) 3780

4. The product of HCF and LCM of 60,84 and 108 is

Answer: d) 45360

5. 108 can be expressed as a product of its primes as

a) 2 3 × 3 2

b) 2 3 × 3 3

c) 2 2 × 3 2

d) 2 2 × 3 3

Answer: d) 2 2 × 3 3

CASE STUDY 3:

A Mathematics Exhibition is being conducted in your School and one of your friends is making a model of a factor tree. He has some difficulty and asks for your help in completing a quiz for the audience.

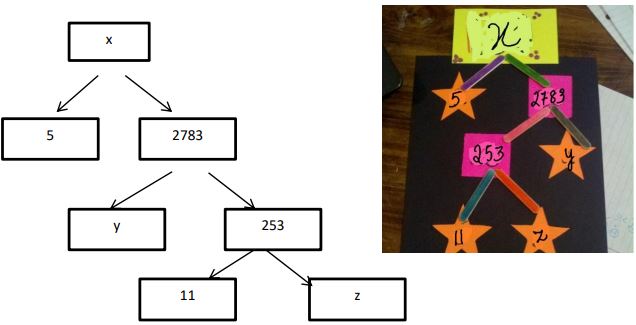
Observe the following factor tree and answer the following:

1. What will be the value of x?

Answer: b) 13915

2. What will be the value of y?

Answer: c) 11

3. What will be the value of z?

Answer: b) 23

4. According to Fundamental Theorem of Arithmetic 13915 is a

a) Composite number

b) Prime number

d) Even number

Answer: a) Composite number

5. The prime factorisation of 13915 is

a) 5 × 11 3 × 13 2

b) 5 × 11 3 × 23 2

c) 5 × 11 2 × 23

d) 5 × 11 2 × 13 2

Answer: c) 5 × 11 2 × 23

Also Check:

CBSE Case Study Questions for Class 10 Maths - All Chapters

Tips to Solve Case Study Based Questions Accurately

Latest Education News

SSC CGL Result 2024 Live: Tier 1 Selection List PDF at ssc.gov.in

BGT 2024-25 Schedule: Team Squads, Match Venues, Time and Where to Watch Live Streaming

Swanath Scholarship 2024: Direct Link to Apply Online, Check Eligibility, Application Process and Benefits

RSMSSB Animal Attendant Admit Card 2024: राजस्थान पशु परिचार एडमिट कार्ड जल्द, जानें कहां और कैसे कर सकेंगे डाउनलोड

DBRAU Admit Card 2024 at dbrau.ac.in; Direct Link to Download UG and PG ODD Semester Hall Ticket PDF

Haryana Board Class 12 Accountancy Model Paper With Solution 2024-25: Download Free PDF

RRB ALP Admit Card 2024: आरआरबी लोको पायलट एडमिट कार्ड जल्द, जानें कहां मिलेगा Direct Download Link

TS TET 2024 Registration Last date Today: Direct Link to Apply Online for Telangana TET Exam at tgtet2024.aptonline.in, Check Details Here

HP Board Class 10 English Model Paper 2024-25: Download FREE PDF

Bihar Board Exam Date 2025: BSEB to Issue Class 10, 12 Time Table Soon at biharboardonline.gov.in

UGC NET December 2024 Notification Out at ugcnet.nta.ac.in: Check Exam Date, Eligibility & Important Dates

Most Wickets By Spinners in BGT: किस फिरकी गेंदबाज ने चटकाए है सर्वाधिक विकेट, यहां देखें सभी के नाम

Optical Illusion IQ Test: Only 2% With Sharp Vision Can Spot The Snail In 5 Seconds!

Men’s Day 2024: What are the Six Objectives of International Men’s Day? Check Key Men’s Issues Here

SSC CGL Result 2024: किसी भी समय जारी हो सकता है सीजीएल का रिजल्ट, यहाँ सबसे पहले मिलेगा लिंक

NEET PG Supreme Court Hearing 2024 Postponed to November 26, Check Latest Updates Here

OSSC CHSL Recruitment 2024 For 324 Soil Conservation Extension Worker Posts: Check Eligibility And Application Process

Why 'Pur' is Written in the Name of Cities and Villages, Check Here

MCC NEET UG Counselling 2024 Special Stray Vacancy Round Begins Today, Check Schedule

BTEUP Revaluation Result 2024 OUT on bteup.ac.in; Direct Link to Download Latest Semester Exam Marksheet PDF

New QB365-SLMS
12th Standard Materials
11th Standard Materials
10th Standard Materials
9th Standard Materials
8th Standard Materials
7th Standard Materials
6th Standard Materials
12th Standard CBSE Materials
11th Standard CBSE Materials
10th Standard CBSE Materials
9th Standard CBSE Materials
8th Standard CBSE Materials
7th Standard CBSE Materials
6th Standard CBSE Materials
Tamilnadu Stateboard
Scholarship Exams
Scholarships

CBSE 10th Standard Maths Subject Case Study Questions With Solution 2021 Part - II

By QB365 on 21 May, 2021

QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams

QB365 - Question Bank Software

10th Standard CBSE

Final Semester - June 2015

Case Study Questions

(ii) Proportional expense for each person is

(iii) The fixed (or constant) expense for the party is

(iv) If there would be 15 guests at the lunch party, then what amount Mr Jindal has to pay?

(v) The system of linear equations representing both the situations will have

(ii) Represent the situation faced by Suman, algebraically

(iii) The price of one Physics book is

(iv) The price of one Mathematics book is

(v) The system of linear equations represented by above situation, has

(ii) Represent algebraically the situation of day- II.

(iii) The linear equation represented by day-I, intersect the x axis at

(iv) The linear equation represented by day-II, intersect the y-axis at

(v) Linear equations represented by day-I and day -II situations, are

Amit is preparing for his upcoming semester exam. For this, he has to practice the chapter of Quadratic Equations. So he started with factorization method. Let two linear factors of \(a x^{2}+b x+c \text { be }(p x+q) \text { and }(r x+s)\) \(\therefore a x^{2}+b x+c=(p x+q)(r x+s)=p r x^{2}+(p s+q r) x+q s .\) Now, factorize each of the following quadratic equations and find the roots. (i) 6x 2 + x - 2 = 0

(ii) 2x 2 -+ x - 300 = 0

(iii) x 2 - 8x + 16 = 0

(iv) 6x 2 - 13x + 5 = 0

(v) 100x 2 - 20x + 1 = 0

(ii) Difference of pairs of shoes in 17 th row and 10 th row is

(iii) On next day, she arranges x pairs of shoes in 15 rows, then x =

(iv) Find the pairs of shoes in 30 th row.

(v) The total number of pairs of shoes in 5 th and 8 th row is

(ii) The number on first card is

(iii) What is the number on the 19 th card?

(iv) What is the number on the 23 rd card?

(v) The sum of numbers on the first 15 cards is

A sequence is an ordered list of numbers. A sequence of numbers such that the difference between the consecutive terms is constant is said to be an arithmetic progression (A.P.). On the basis of above information, answer the following questions. (i) Which of the following sequence is an A.P.?

(ii) If x, y and z are in A.P., then

(iii) If a 1 a 2 , a 3 ..... , a n are in A.P., then which of the following is true?

(iv) If the n th term (n > 1) of an A.P. is smaller than the first term, then nature of its common difference (d) is

(v) Which of the following is incorrect about A.P.?

(ii) Find the radius of the core.

(iii) S 2 =

(iv) What is the diameter of roll when one tissue sheet is rolled over it?

(v) Find the thickness of each tissue sheet

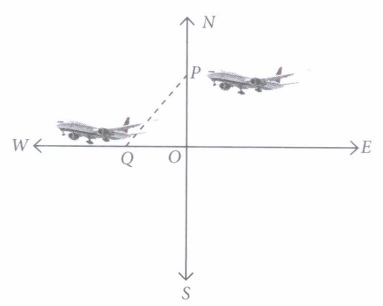
(ii) Distance travelled by aeroplane towards west after \(1 \frac{1}{2}\) hr is

(iii) In the given figure, \(\angle\) POQ is

(iv) Distance between aeroplanes after \(1 \frac{1}{2}\) hr is

(v) Area of \(\Delta\) POQ is

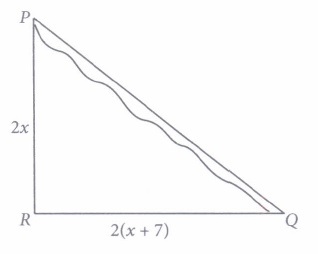
(ii) The value of x is

(iii) The value of PR is

(iv) The value of RQ is

(v) How much distance will be saved in reaching city Q after the construction of highway?

(ii) Length of BC =

(iii) Length of AD =

(iv) Length of ED =

(v) Length of AE =

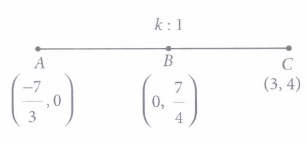
(ii) The value of x + y is

(iii) Which of the following is true?

(iv) The ratio in which B divides AC is

(v) Which of the following equations is satisfied by the given points?

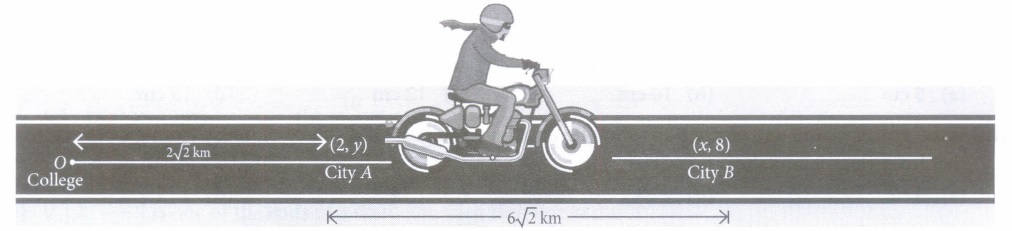
(ii) The value of x is equal to

(iii) If M is any point exactly in between city A and city B, then coordinates of M are

(iv) The ratio in which A divides the line segment joining the points O and M is

(v) If the person analyse the petrol at the point M(the mid point of AB), then what should be his decision?

(ii) The centre of circle is the

(iii) The radius of the circle is

(iv) The area of the circle is

(v) If \(\left(1, \frac{\sqrt{7}}{3}\right)\) is one of the ends of a diameter, then its other end is

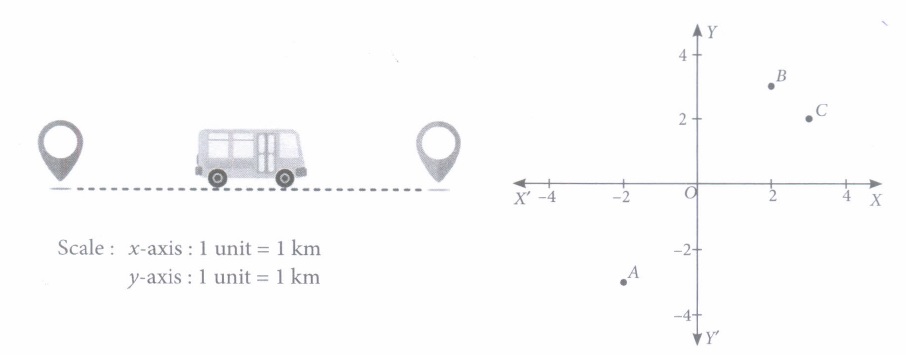
(ii) The distance between A and Cis

(iii) If it is assumed that both buses have same speed, then by which bus do you want to travel from A to B?

(iv) If the fare for first bus is Rs10/km, then what will be the fare for total journey by that bus?

(v) If the fare for second bus is Rs 15/km, then what will be the fare to reach to the destination by this bus?

*****************************************

Cbse 10th standard maths subject case study questions with solution 2021 part - ii answer keys.

(i) (a): 1 st situation can be represented as x + 7y = 650 ...(i) and 2 nd situation can be represented as x + 11y = 970 ...(ii) (ii) (b): Subtracting equations (i) from (ii), we get \(4 y=320 \Rightarrow y=80\) \(\therefore\) Proportional expense for each person is Rs 80. (iii) (c): Puttingy = 80 in equation (i), we get x + 7 x 80 = 650 \(\Rightarrow\) x = 650 - 560 = 90 \(\therefore\) Fixed expense for the party is Rs 90 (iv) (d): If there will be 15 guests, then amount that Mr Jindal has to pay = Rs (90 + 15 x 80) = Rs 1290 (v) (a): We have a 1 = 1, b 1 = 7, c 1 = -650 and \(a_{2}=1, b_{2}=11, c_{2}=-970 \) \(\therefore \frac{a_{1}}{a_{2}}=1, \frac{b_{1}}{b_{2}}=\frac{7}{11}, \frac{c_{1}}{c_{2}}=\frac{-650}{-970}=\frac{65}{97}\) \(\text { Here, } \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) Thus, system of linear equations has unique solution.

(i) (a): Situation faced by Sudhir can be represented algebraically as 2x + 3y = 850 (ii) (b): Situation faced by Suman can be represented algebraically as 3x + 2y = 900 (iii) (c) : We have 2x + 3y = 850 .........(i) and 3x + 2y = 900 .........(ii) Multiplying (i) by 3 and (ii) by 2 and subtracting, we get 5y = 750 \(\Rightarrow\) Y = 150 Thus, price of one Physics book is Rs 150. (iv) (d): From equation (i) we have, 2x + 3 x 150 = 850 \(\Rightarrow\) 2x = 850 - 450 = 400 \(\Rightarrow\) x = 200 Hence, cost of one Mathematics book = Rs 200 (v) (a): From above, we have \(a_{1} =2, b_{1}=3, c_{1}=-850 \) \(\text { and } a_{2} =3, b_{2}=2, c_{2}=-900\) \(\therefore \quad \frac{a_{1}}{a_{2}}=\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{3}{2}, \frac{c_{1}}{c_{2}}=\frac{-850}{-900}=\frac{17}{18} \Rightarrow \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) Thus system of linear equations has unique solution.

(i) (b): Algebraic representation of situation of day-I is 2x + y = 1600. (ii) (a): Algebraic representation of situation of day- II is 4x + 2y = 3000 \(\Rightarrow\) 2x + y = 1500. (iii) (c) : At x-axis, y = 0 \(\therefore\) At y = 0, 2x + y = 1600 becomes 2x = 1600 \(\Rightarrow\) x = 800 \(\therefore\) Linear equation represented by day- I intersect the x-axis at (800, 0). (iv) (d) : At y-axis, x = 0 \(\therefore\) 2x + Y = 1500 \(\Rightarrow\) y = 1500 \(\therefore\) Linear equation represented by day-II intersect the y-axis at (0, 1500). (v) (b): We have, 2x + y = 1600 and 2x + y = 1500 Since \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \text { i.e., } \frac{1}{1}=\frac{1}{1} \neq \frac{16}{15}\) \(\therefore\) System of equations have no solution. \(\therefore\) Lines are parallel.

(i) (b): We have \(6 x^{2}+x-2=0\) \(\Rightarrow \quad 6 x^{2}-3 x+4 x-2=0 \) \(\Rightarrow \quad(3 x+2)(2 x-1)=0 \) \(\Rightarrow \quad x=\frac{1}{2}, \frac{-2}{3}\) (ii) (c): \(2 x^{2}+x-300=0\) \(\Rightarrow \quad 2 x^{2}-24 x+25 x-300=0 \) \(\Rightarrow \quad(x-12)(2 x+25)=0 \) \(\Rightarrow \quad x=12, \frac{-25}{2}\) (iii) (d): \(x^{2}-8 x+16=0\) \(\Rightarrow(x-4)^{2}=0 \Rightarrow(x-4)(x-4)=0 \Rightarrow x=4,4\) (iv) (d): \(6 x^{2}-13 x+5=0\) \(\Rightarrow \quad 6 x^{2}-3 x-10 x+5=0 \) \(\Rightarrow \quad(2 x-1)(3 x-5)=0 \) \(\Rightarrow \quad x=\frac{1}{2}, \frac{5}{3}\) (v) (a): \(100 x^{2}-20 x+1=0\) \(\Rightarrow(10 x-1)^{2}=0 \Rightarrow x=\frac{1}{10}, \frac{1}{10}\)

Number of pairs of shoes in 1 st , 2 nd , 3 rd row, ... are 3,5,7, ... So, it forms an A.P. with first term a = 3, d = 5 - 3 = 2 (i) (d): Let n be the number of rows required. \(\therefore S_{n}=120 \) \(\Rightarrow \quad \frac{n}{2}[2(3)+(n-1) 2]=120 \) \(\Rightarrow \quad n^{2}+2 n-120=0 \Rightarrow n^{2}+12 n-10 n-120=0\) \(\Rightarrow \quad(n+12)(n-10)=0 \Rightarrow n=10\) So, 10 rows required to put 120 pairs. (ii) (b): No. of pairs in 1ih row = t 17 = 3 + 16(2) = 35 No. of pairs in 10th row = t 10 = 3 + 9(2) = 21 \(\therefore\) Required difference = 35 - 21 = 14 (iii) (c) : Here n = 15 \(\therefore\) t 15 = 3 + 14(2) = 3 + 28 = 31 (iv) (a): No. of pairs in 30 th row = t 30 = 3 +29(2) = 61 (v) (c): No. of pairs in 5 th row = t 5 = 3 + 4(2) = 11 No. of pairs in 8 th row = t 8 = 3 + 7(2) = 17 \(\therefore\) Required sum = 11 + 17 = 28

Let the numbers on the cards be a, a + d, a + Zd, ... According to question, We have (a + 5d) + (a + 13d) = -76 \(\Rightarrow\) 2a+18d = -76 \(\Rightarrow\) a + 9d= -38 ... (1) And (a + 7d) + (a + 15d) = -96 \(\Rightarrow\) 2a + 22d = -96 \(\Rightarrow\) a + 11d = -48 ...(2) From (1) and (2), we get 2d= -10 \(\Rightarrow\) d= -5 From (1), a + 9(-5) = -38 \(\Rightarrow\) a = 7 (i) (b): The difference between the numbers on any two consecutive cards = common difference of the A.P.=-5 (ii) (d): Number on first card = a = 7 (iii) (b): Number on 19th card = a + 18d = 7 + 18(-5) = -83 (iv) (a): Number on 23rd card = a + 22d = 7 + 22( -5) = -103 (v) (d): \(S_{15}=\frac{15}{2}[2(7)+14(-5)]=-420\)

(i) (c) (ii) (c) (iii) (d) (iv) (b) (v) (c)

Here S n = 0.1n 2 + 7.9n (i) (c): S n -1 = 0.1(n - 1) 2 + 7.9(n - 1) = 0.1n 2 + 7.7n - 7.8 (ii) (b): S 1 = t 1 = a = 0.1(1) 2 + 7.9(1) = 8 cm = Diameter of core So, radius of the core = 4 cm (iii) (a): S 2 = 0.1(2) 2 + 7.9(2) = 16.2 (iv) (d): Required diameter = t 2 = S 2 - S 1 = 16.2 - 8 = 8.2 cm (v) (c): As d = t 2 - t 1 = 8.2 - 8 = 0.2 cm So, thickness of tissue = 0.2 \(\div\) 2 = 0.1 cm = 1 mm

(i) (a): Speed = 1200 km/hr \(\text { Time }=1 \frac{1}{2} \mathrm{hr}=\frac{3}{2} \mathrm{hr}\) \(\therefore\) Required distance = Speed x Time \(=1200 \times \frac{3}{2}=1800 \mathrm{~km}\) (ii) (c): Speed = 1500 km/hr Time = \(\frac{3}{2}\) hr. \(\therefore\) Required distance = Speed x Time \(=1500 \times \frac{3}{2}=2250 \mathrm{~km}\) (iii) (b): Clearly, directions are always perpendicular to each other. \(\therefore \quad \angle P O Q=90^{\circ}\) (iv) (a): Distance between aeroplanes after \(1\frac{1}{2}\) hour \(\begin{array}{l} =\sqrt{(1800)^{2}+(2250)^{2}}=\sqrt{3240000+5062500} \\ =\sqrt{8302500}=450 \sqrt{41} \mathrm{~km} \end{array}\) (v) (d): Area of \(\Delta\) POQ= \(\frac{1}{2}\) x base x height \(=\frac{1}{2} \times 2250 \times 1800=2250 \times 900=2025000 \mathrm{~km}^{2}\)

(i) (b) (ii) (c): Using Pythagoras theorem, we have PQ 2 = PR 2 + RQ 2 \(\Rightarrow(26)^{2}=(2 x)^{2}+(2(x+7))^{2} \Rightarrow 676=4 x^{2}+4(x+7)^{2} \) \(\Rightarrow 169=x^{2}+x^{2}+49+14 x \Rightarrow x^{2}+7 x-60=0\) \(\Rightarrow x^{2}+12 x-5 x-60=0 \) \(\Rightarrow x(x+12)-5(x+12)=0 \Rightarrow(x-5)(x+12)=0 \) \(\Rightarrow x=5, x=-12\) \(\therefore \quad x=5\) [Since length can't be negative] (iii) (a) : PR = 2x = 2 x 5 = 10 km (iv) (b): RQ= 2(x + 7) = 2(5 + 7) = 24 km (v) (d): Since, PR + RQ = 10 + 24 = 34 km Saved distance = 34 - 26 = 8 km

(i) (b): If \(\Delta\) AED and \(\Delta\) BEC, are similar by SAS similarity rule, then their corresponding proportional sides are \(\frac{B E}{A E}=\frac{C E}{D E}\) (ii) (c): By Pythagoras theorem, we have \(\begin{array}{l} B C=\sqrt{C E^{2}+E B^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{16+9} \\ =\sqrt{25}=5 \mathrm{~cm} \end{array}\) (iii) (a): Since \(\Delta\) ADE and \(\Delta\) BCE are similar. \(\therefore \quad \frac{\text { Perimeter of } \triangle A D E}{\text { Perimeter of } \Delta B C E}=\frac{A D}{B C} \) \(\Rightarrow \frac{2}{3}=\frac{A D}{5} \Rightarrow A D=\frac{5 \times 2}{3}=\frac{10}{3} \mathrm{~cm}\) (iv) (b): \(\frac{\text { Perimeter of } \triangle A D E}{\text { Perimeter of } \Delta B C E}=\frac{E D}{C E} \) \(\Rightarrow \frac{2}{3}=\frac{E D}{4} \Rightarrow E D=\frac{4 \times 2}{3}=\frac{8}{3} \mathrm{~cm}\) (v) (d) : \(\frac{\text { Perimeter of } \Delta A D E}{\text { Perimeter of } \Delta B C E}=\frac{A E}{B E} \Rightarrow \frac{2}{3} B E=A E\) \(\Rightarrow A E=\frac{2}{3} \sqrt{B C^{2}-C E^{2}} \) \(\text { Also, in } \triangle A E D, A E=\sqrt{A D^{2}-D E^{2}}\)

(i) (a): We have, OA = 2 \(\sqrt{2}\) km \(\Rightarrow \sqrt{2^{2}+y^{2}}=2 \sqrt{2} \) \(\Rightarrow 4+y^{2}=8 \Rightarrow y^{2}=4 \) \(\Rightarrow y=2 \quad(\because y=-2 \text { is not possible })\) (ii) (c): We have OB = 8 \(\sqrt{2}\) \(\Rightarrow \sqrt{x^{2}+8^{2}}=8 \sqrt{2} \) \(\Rightarrow x^{2}+64=128 \Rightarrow x^{2}=64 \) \(\Rightarrow x=8 \quad(\because x=-8 \text { is not possible })\) (iii) (c) : Coordinates of A and Bare (2, 2) and (8, 8) respectively, therefore coordinates of point M are \(\left(\frac{2+8}{2}, \frac{2+8}{2}\right)\) i.e .,(5.5) (iv) (d): Let A divides OM in the ratio k: 1.Then \(2=\frac{5 k+0}{k+1} \Rightarrow 2 \mathrm{k}+2=5 k \Rightarrow 3 k=2 \Rightarrow k=\frac{2}{3}\) \(\therefore\) Required ratio = 2 : 3 (v) (b): Since M is the mid-point of A and B therefore AM = MB. Hence, he should try his luck moving towards B.

(i) (c): Required coordinates are \(\left(0, \frac{4}{3}\right)\) (ii) (c) (iii) (a): Radius = Distance between (0,0) and \(\left(\frac{4}{3}, 0\right)\) \(=\sqrt{\left(\frac{4}{3}\right)^{2}+0^{2}}=\frac{4}{3} \text { units }\) (iv) (b): Area of circle = \(\pi\) (radius) 2 \(=\pi\left(\frac{4}{3}\right)^{2}=\frac{16}{9} \pi \text { sq. units }\) (v) (d): Let the coordinates of the other end be (x,y). Then (0,0) will bethe mid-point of \(\left(1, \frac{\sqrt{7}}{3}\right)\) and (x, y). \(\therefore\left(\frac{1+x}{2}, \frac{\frac{\sqrt{7}}{3}+y}{2}\right)=(0,0) \) \(\Rightarrow \frac{1+x}{2}=0 \text { and } \frac{\frac{\sqrt{7}}{3}+y}{2}=0 \) \(\Rightarrow x=-1 \text { and } y=-\frac{\sqrt{7}}{3}\) Thus, the coordinates of other end be \(\left(-1, \frac{-\sqrt{7}}{3}\right)\)

Coordinates of A, Band Care (-2, -3), (2, 3) and (3,2). (i) (d): Required distance \(=\sqrt{(2+2)^{2}+(3+3)^{2}}\) \(=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=2 \sqrt{13} \mathrm{~km} \approx 7.2 \mathrm{~km}\) (ii) (d): Required distance \(=\sqrt{(3+2)^{2}+(2+3)^{2}}\) \(=\sqrt{5^{2}+5^{2}}=5 \sqrt{2} \mathrm{~km}\) (iii) (b): Distance between Band C \(=\sqrt{(3-2)^{2}+(2-3)^{2}}=\sqrt{1+1}=\sqrt{2} \mathrm{~km}\) Thus, distance travelled by first bus to reach to B \(=A C+C B=5 \sqrt{2}+\sqrt{2}=6 \sqrt{2} \mathrm{~km} \approx 8.48 \mathrm{~km}\) and distance travelled by second bus to reach to B \(=A B=2 \sqrt{13} \mathrm{~km} \approx 7.2 \mathrm{~km}\) \(\therefore\) Distance of first bus is greater than distance of the second bus, therefore second bus should be chosen. (iv) (d): Distance travelled by first bus = 8.48 km \(\therefore\) Total fare = 8.48 x 10 = Rs 84.80 (v) (b): Distance travelled by second bus = 7. 2 km \(\therefore\) Total fare = 7.2 x 15 = Rs 108

Related 10th Standard CBSE Maths Materials

10th standard cbse syllabus & materials, cbse 10th social science the making of a global world chapter case study question with answers, cbse 10th social science nationalism in india chapter case study question with answers, cbse 10th social science the rise of nationalism in europe chapter case study question with answers, cbse 10th science metals and non metals chapter case study question with answers, cbse 10th science acids, bases and salts chapter case study question with answers, cbse 10th science chemical reactions and equations chapter case study question with answers, class 10th science - our environment case study questions and answers 2022 - 2023, class 10th science - magnetic effects of electric current case study questions and answers 2022 - 2023, class 10th science - electricity case study questions and answers 2022 - 2023, class 10th science - human eye and the colourful world case study questions and answers 2022 - 2023, class 10th science - light reflection and refraction case study questions and answers 2022 - 2023, class 10th science - heredity and evolution case study questions and answers 2022 - 2023, class 10th science - how do organisms reproduce case study questions and answers 2022 - 2023, class 10th science - life processes case study questions and answers 2022 - 2023, class 10th science - periodic classification of elements case study questions and answers 2022 - 2023.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

10th Standard CBSE Study Materials

10th Standard CBSE Subjects

IMAGES

Case Study base Class 10 Maths Questions
CASE STUDY Class 10 Maths Basic Sample Paper 2021 SOLVED |Basic Math
Case Study Class 10 Maths CBSE Question Bank Solution Probability Case
CBSE Class 10
Class 10
Case study based Questions class 10 I case study based questions on

VIDEO

How to Solve Case Study in MINIMUM Time like a Pro!🔥 Class 12 Maths
Consistency Study #study #shorts #sciencer
The Secret Study Trick! 🔥 Score 95+ in Class 9
Case Study Questions for CBSE Class 12th Maths Board Exam 2024 @AkashDashClasses
9th Class Test Topper I MathZone Short Video
cbse class 10 mathematics real number ex1.1। number system classes by sunil kumar sharma ।10th math।