

Rich Problems – Part 1
Rich problems – part 1, by marvin cohen and karen rothschild.
One of the underlying beliefs that guides Math for All is that in order to learn mathematics well, students must engage with rich problems. Rich problems allow ALL students, with a variety of neurodevelopmental strengths and challenges, to engage in mathematical reasoning and become flexible and creative thinkers about mathematical ideas. In this Math for All Updates, we review what rich problems are, why they are important, and where to find some ready to use. In a later Math for All Updates we will discuss how to create your own rich problems customized for your curriculum.
What are Rich Problems?
At Math for All, we believe that all rich problems provide:
- opportunities to engage the problem solver in thinking about mathematical ideas in a variety of non-routine ways.
- an appropriate level of productive struggle.
- an opportunity for students to communicate their thinking about mathematical ideas.
Rich problems increase both the problem solver’s reasoning skills and the depth of their mathematical understanding. Rich problems are rich because they are not amenable to the application of a known algorithm, but require non-routine use of the student’s knowledge, skills, and ingenuity. They usually offer multiple entry pathways and methods of representation. This provides students with diverse abilities and challenges the opportunity to create solution strategies that leverage their particular strengths.
Rich problems usually have one or more of the following characteristics:
- Several correct answers. For example, “Find four numbers whose sum is 20.”
- A single answer but with many pathways to a solution. For example, “There are 10 animals in the barnyard, some chickens, some pigs. Altogether there are 24 legs. How many of the animals are chickens and how many are pigs?”
- A level of complexity that may require an entire class period or more to solve.
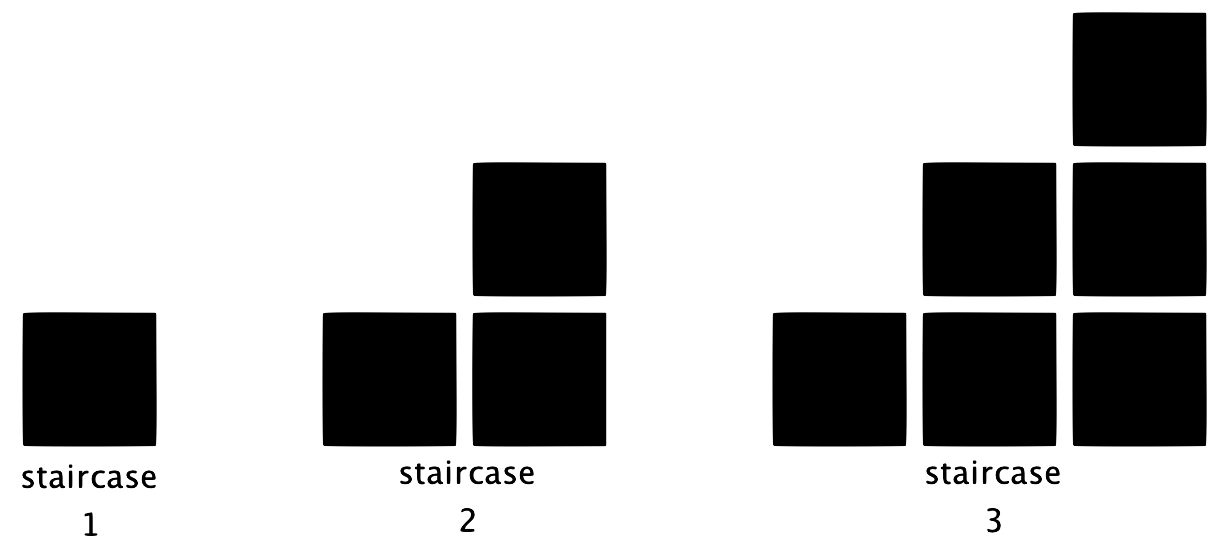
- An opportunity to look for patterns and make connections to previous problems, other students’ strategies, and other areas of mathematics. For example, see the staircase problem below.
- A “low floor and high ceiling,” meaning both that all your students will be able to engage with the mathematics of the problem in some way, and that the problem has sufficient complexity to challenge all your students. NRICH summarizes this approach as “everyone can get started, and everyone can get stuck” (2013). For example, a problem could have a variety of questions related to the following sequence, such as: How many squares are in the next staircase? How many in the 20th staircase? What is the rule for finding the number of squares in any staircase?
- An expectation that the student be able to communicate their ideas and defend their approach.
- An opportunity for students to choose from a range of tools and strategies to solve the problem based on their own neurodevelopmental strengths.
- An opportunity to learn some new mathematics (a mathematical residue) through working on the problem.
- An opportunity to practice routine skills in the service of engaging with a complex problem.
- An opportunity for a teacher to deepen their understanding of their students as learners and to build new lessons based on what students know, their developmental level, and their neurodevelopmental strengths and challenges.
Why Rich Problems?
All adults need mathematical understanding to solve problems in their daily lives. Most adults use calculators and computers to perform routine computation beyond what they can do mentally. They must, however, understand enough mathematics to know what to enter into the machines and how to evaluate what comes out. Our personal financial situations are deeply affected by our understanding of pricing schemes for the things we buy, the mortgages we hold, and fees we pay. As citizens, understanding mathematics can help us evaluate government policies, understand political polls, and make decisions. Building and designing our homes, and scaling up recipes for crowds also require math. Now especially, mathematical understanding is crucial for making sense of policies related to the pandemic. Decisions about shutdowns, medical treatments, and vaccines are all grounded in mathematics. For all these reasons, it is important students develop their capacities to reason about mathematics. Research has demonstrated that experience with rich problems improves children’s mathematical reasoning (Hattie, Fisher, & Frey, 2017).
Where to Find Rich Problems
Several types of rich problems are available online, ready to use or adapt. The sites below are some of many places where rich problems can be found:
- Which One Doesn’t Belong – These problems consist of squares divided into 4 quadrants with numbers, shapes, or graphs. In every problem there is at least one way that each of the quadrants “doesn’t belong.” Thus, any quadrant can be argued to be different from the others.
- “Open Middle” Problems – These are problems with a single answer but with many ways to reach the answer. They are organized by both topic and grade level.
- NRICH Maths – This is a multifaceted site from the University of Cambridge in Great Britain. It has both articles and ready-made problems. The site includes problems for grades 1–5 (scroll down to the “Collections” section) and problems for younger children . We encourage you to explore NRICH more fully as well. There are many informative articles and discussions on the site.
- Rich tasks from Virginia – These are tasks published by the Virginia Department of education. They come with complete lesson plans as well as example anticipated student responses.
- Rich tasks from Georgia – This site contains a complete framework of tasks designed to address all standards at all grades. They include 3-Act Tasks , YouCubed Tasks , and many other tasks that are open ended or feature an open middle approach.
The problems can be used “as is” or adapted to the specific neurodevelopmental strengths and challenges of your students. Carefully adapted, they can engage ALL your students in thinking about mathematical ideas in a variety of ways, thereby not only increasing their skills but also their abilities to think flexibly and deeply.
Hattie, J., Fisher, D., & Frey, N. (2017). Visible learning for mathematics, grades K-12: What works best to optimize student learning. Thousand Oaks, CA: Corwin Mathematics.
NRICH Team. (2013). Low Threshold High Ceiling – an Introduction . Cambridge University, United Kingdom: NRICH Maths.
The contents of this blog post were developed under a grant from the Department of Education. However, those contents do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.
Math for All is a professional development program that brings general and special education teachers together to enhance their skills in planning and adapting mathematics lessons to ensure that all students achieve high-quality learning outcomes in mathematics.
Our Newsletter Provides Ideas for Making High-Quality Mathematics Instruction Accessible to All Students
Sign up for our newsletter, recent blogs.
- Social Justice in the Math Classroom May 30, 2024
- Parents and Teachers as Co-Constructors of Children’s Success as Mathematical Learners May 1, 2024
- The Problem with Word Problems March 11, 2024
- Honoring Diversity: What, why, and how? February 22, 2024
- Looking at a Student at Work January 3, 2024
Team & Partners
Testimonials
Newsletter Signup
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Additional menu
Khan Academy Blog
Free Math Worksheets — Over 100k free practice problems on Khan Academy
Looking for free math worksheets.
You’ve found something even better!
That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!
Just choose your grade level or topic to get access to 100% free practice questions:
Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.
- Trigonometry

Statistics and probability
High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.
- Addition and subtraction
- Place value (tens and hundreds)
- Addition and subtraction within 20
- Addition and subtraction within 100
- Addition and subtraction within 1000
- Measurement and data
- Counting and place value
- Measurement and geometry
- Place value
- Measurement, data, and geometry
- Add and subtract within 20
- Add and subtract within 100
- Add and subtract within 1,000
- Money and time
- Measurement
- Intro to multiplication
- 1-digit multiplication
- Addition, subtraction, and estimation
- Intro to division
- Understand fractions
- Equivalent fractions and comparing fractions
- More with multiplication and division
- Arithmetic patterns and problem solving
- Quadrilaterals
- Represent and interpret data
- Multiply by 1-digit numbers
- Multiply by 2-digit numbers
- Factors, multiples and patterns
- Add and subtract fractions
- Multiply fractions
- Understand decimals
- Plane figures
- Measuring angles
- Area and perimeter
- Units of measurement
- Decimal place value
- Add decimals
- Subtract decimals
- Multi-digit multiplication and division
- Divide fractions
- Multiply decimals
- Divide decimals
- Powers of ten
- Coordinate plane
- Algebraic thinking
- Converting units of measure
- Properties of shapes
- Ratios, rates, & percentages
- Arithmetic operations
- Negative numbers
- Properties of numbers
- Variables & expressions
- Equations & inequalities introduction
- Data and statistics
- Negative numbers: addition and subtraction
- Negative numbers: multiplication and division
- Fractions, decimals, & percentages
- Rates & proportional relationships
- Expressions, equations, & inequalities
- Numbers and operations
- Solving equations with one unknown
- Linear equations and functions
- Systems of equations
- Geometric transformations
- Data and modeling
- Volume and surface area
- Pythagorean theorem
- Transformations, congruence, and similarity
- Arithmetic properties
- Factors and multiples
- Reading and interpreting data
- Negative numbers and coordinate plane
- Ratios, rates, proportions
- Equations, expressions, and inequalities
- Exponents, radicals, and scientific notation
- Foundations
- Algebraic expressions
- Linear equations and inequalities
- Graphing lines and slope
- Expressions with exponents
- Quadratics and polynomials
- Equations and geometry
- Algebra foundations
- Solving equations & inequalities
- Working with units
- Linear equations & graphs
- Forms of linear equations
- Inequalities (systems & graphs)
- Absolute value & piecewise functions
- Exponents & radicals
- Exponential growth & decay
- Quadratics: Multiplying & factoring
- Quadratic functions & equations
- Irrational numbers
- Performing transformations
- Transformation properties and proofs
- Right triangles & trigonometry
- Non-right triangles & trigonometry (Advanced)
- Analytic geometry
- Conic sections
- Solid geometry
- Polynomial arithmetic
- Complex numbers
- Polynomial factorization
- Polynomial division
- Polynomial graphs
- Rational exponents and radicals
- Exponential models
- Transformations of functions
- Rational functions
- Trigonometric functions
- Non-right triangles & trigonometry
- Trigonometric equations and identities
- Analyzing categorical data
- Displaying and comparing quantitative data
- Summarizing quantitative data
- Modeling data distributions
- Exploring bivariate numerical data
- Study design
- Probability
- Counting, permutations, and combinations
- Random variables
- Sampling distributions
- Confidence intervals
- Significance tests (hypothesis testing)
- Two-sample inference for the difference between groups
- Inference for categorical data (chi-square tests)
- Advanced regression (inference and transforming)
- Analysis of variance (ANOVA)
- Scatterplots
- Data distributions
- Two-way tables
- Binomial probability
- Normal distributions
- Displaying and describing quantitative data
- Inference comparing two groups or populations
- Chi-square tests for categorical data
- More on regression
- Prepare for the 2020 AP®︎ Statistics Exam
- AP®︎ Statistics Standards mappings
- Polynomials
- Composite functions
- Probability and combinatorics
- Limits and continuity
- Derivatives: definition and basic rules
- Derivatives: chain rule and other advanced topics
- Applications of derivatives
- Analyzing functions
- Parametric equations, polar coordinates, and vector-valued functions
- Applications of integrals
- Differentiation: definition and basic derivative rules
- Differentiation: composite, implicit, and inverse functions
- Contextual applications of differentiation
- Applying derivatives to analyze functions
- Integration and accumulation of change
- Applications of integration
- AP Calculus AB solved free response questions from past exams
- AP®︎ Calculus AB Standards mappings
- Infinite sequences and series
- AP Calculus BC solved exams
- AP®︎ Calculus BC Standards mappings
- Integrals review
- Integration techniques
- Thinking about multivariable functions
- Derivatives of multivariable functions
- Applications of multivariable derivatives
- Integrating multivariable functions
- Green’s, Stokes’, and the divergence theorems
- First order differential equations
- Second order linear equations
- Laplace transform
- Vectors and spaces
- Matrix transformations
- Alternate coordinate systems (bases)
Frequently Asked Questions about Khan Academy and Math Worksheets
Why is khan academy even better than traditional math worksheets.
Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.
| Math Worksheets | Khan Academy |
|---|---|
| Math worksheets take forever to hunt down across the internet | Khan Academy is your one-stop-shop for practice from arithmetic to calculus |
| Math worksheets can vary in quality from site to site | Every Khan Academy question was written by a math expert with a strong education background |
| Math worksheets can have ads or cost money | Khan Academy is a nonprofit whose resources are always free to teachers and learners – no ads, no subscriptions |
| Printing math worksheets use up a significant amount of paper and are hard to distribute during virtual learning | Khan Academy practice requires no paper and can be distributed whether your students are in-person or online |
| Math worksheets can lead to cheating or a lack of differentiation since every student works on the same questions | Khan Academy has a full question bank to draw from, ensuring that each student works on different questions – and at their perfect skill level |
| Math worksheets can slow down student learning since they need to wait for feedback | Khan Academy gives instant feedback after every answer – including hints and video support if students are stuck |
| Math worksheets take up time to collect and take up valuable planning time to grade | Khan Academy questions are graded instantly and automatically for you |
What do Khan Academy’s interactive math worksheets look like?
Here’s an example:
What are teachers saying about Khan Academy’s interactive math worksheets?
“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”
Is Khan Academy free?
Khan Academy’s practice questions are 100% free—with no ads or subscriptions.
What do Khan Academy’s interactive math worksheets cover?
Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.
Is Khan Academy a company?
Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.
Want to get even more out of Khan Academy?
Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.
Get Khanmigo
The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo.
For learners For teachers For parents
As a nonprofit, we need your support to provide a free, world-class education to anyone, anywhere.

IMAGES
VIDEO