

We apologize for the inconvenience...
To ensure we keep this website safe, please can you confirm you are a human by ticking the box below.
If you are unable to complete the above request please contact us using the below link, providing a screenshot of your experience.
https://ioppublishing.org/contacts/

- Simple Search
- Advanced Search
- Deposit an Item
- Deposit Instructions
- Instructions for Students
Thesis Files
Repository Staff Only: item control page
Recursive Tight-Binding Green’s Function Method: Application to Ballistic and Dissipative Transport in Semiconductor Nanostructures
Cite this chapter.

- Fernando Sols 5
Part of the book series: NATO ASI Series ((NSSB,volume 342))
576 Accesses
1 Citations
The purpose of this chapter is to present a specific numerical application of Green’s functions in tight-binding structures. The numerical technique is conventionally called the recursive Green’s function method. It was first introduced by ( 1981 ) to study electron transport in disordered systems and, since then, it has been widely used by many authors as a practical tool to simulate quantum transport in a variety of structures. The Green’s function must be defined in a tight-binding structure, which means that the space must be discretized in sites that represent either real atoms with strongly localized orbitals, or fictitious sites that fill the space with a sufficiently high density. The use of tight-binding Green’s functions (TBGF’s) has some practical advantages. For example, hard-wall boundary conditions are simply simulated by the absence of sites. Impurities are conveniently included by introducing sites with unequal diagonal energy. In particular, diagonal disorder may be introduced by making the site energy a random variable. It is also useful for describing transport in geometries with hard-wall boundaries defined by straight segments and right angles (or angles whose tangent is the ratio of low integers). Among its possible shortcomings, we may mention that the recursive TBGF method is not particularly suited to study transport in structures defined by geometrical parameters one may want to vary continously, such as the angle between two wires or the length of a given segment. For this type of purposes, a wave-function matching method ( Schult et al., 1989 ) may be more advantageous [see, for example, ( 1990 ) for a study of electron transport through a circular bend linking two leads with an arbitrary angle]. Within a recursive TBGF scheme, these difficulties can be overcome in principle by introducing a sufficiently dense grid, but the computational cost may easily become prohibitive.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
- Durable hardcover edition
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Unable to display preview. Download preview PDF.
Similar content being viewed by others
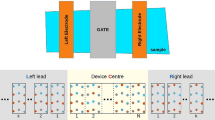
Recursive Green’s functions optimized for atomistic modelling of large superlattice-based devices
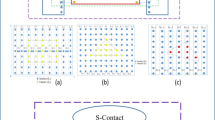
A tutorial on the NEGF method for electron transport in devices and defective materials


Quasiparticle Self-Consistent GW Method for the Spectral Properties of Complex Materials
Baranger, H. U., DiVincenzo, D. P., Jalabert, R. A., and Stone, A. D., 1991, Phys. Rev. B 44:10367.
Article Google Scholar
Büttiker, M. 1986, Phys. Rev. Lett. 57:1761.
Article ADS Google Scholar
Caldeira, A. O., and Leggett, A. J., 1983, Ann. Phys. (N.Y.) 149:374.
Ferry, D. K., and Grubin, H. L., 1994, Solid State Physics , to be published.
Google Scholar
Fisher, D. S., and Lee, P. A., 1981, Phys. Rev. B 23:6851.
Article MathSciNet ADS Google Scholar
MacKinnon, A., 1985, Z. Phys. B 59:385.
Meir, Y., and Wingreen, N.S., 1992, Phys. Rev. Lett. 68:2512
Pevzner, V., Sols, F., and Hess, K., 1991, in “Granular Nanoelectronics”, J. R. Barker, D. K. Ferry, and C. Jacoboni, eds., Plenum, New York.
Schult, R. L., Ravennati, D. G., and Wyld, H. W., 1989, Phys. Rev. B 39:5476.
Sols, F., Macucci, M., Ravaioli, U., and Hess, K., 1989, J. Appl. Phys. 66:3892.
Sols, F., and Macucci, M., 1990, Phys.Rev. B 41:11887.
Sols, F., 1992, Ann. Phys. (N.Y.) 214:386.
Sols, F., 1993, in: “Phonons in semiconductor nanostructures”, J. P. Leburton, J. Pascual, and C. M. Sotomayor-Torres, eds., Kluwer, Norwall, CT.
Stone, A. D., and Szafer, A., 1988, IBM J. Res. Develop . 32:384.
Thouless, D. J., and Kirkpatrick, S., 1981, J. Phys. C 14:235.
Download references
Author information
Authors and affiliations.
Departamento de Física de la Materia Condensada, C-XII, Universidad Autónoma de Madrid, Cantoblanco, E-28049, Madrid, Spain
Fernando Sols
You can also search for this author in PubMed Google Scholar
Editor information
Editors and affiliations.
Arizona State University, Tempe, Arizona, USA
David K. Ferry
SRA, Inc., Glastonbury, Connecticut, USA
Harold L. Grubin
University of Modena, Modena, Italy
Carlo Jacoboni
Technical University of Denmark, Lyngby, Denmark
Anti-Pekka Jauho
Rights and permissions
Reprints and permissions
Copyright information
© 1995 Springer Science+Business Media New York
About this chapter
Sols, F. (1995). Recursive Tight-Binding Green’s Function Method: Application to Ballistic and Dissipative Transport in Semiconductor Nanostructures. In: Ferry, D.K., Grubin, H.L., Jacoboni, C., Jauho, AP. (eds) Quantum Transport in Ultrasmall Devices. NATO ASI Series, vol 342. Springer, Boston, MA. https://doi.org/10.1007/978-1-4615-1967-6_16
Download citation
DOI : https://doi.org/10.1007/978-1-4615-1967-6_16
Publisher Name : Springer, Boston, MA
Print ISBN : 978-1-4613-5809-1
Online ISBN : 978-1-4615-1967-6
eBook Packages : Springer Book Archive
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research

IMAGES
VIDEO
COMMENTS
Introduction to Green functions and many-body perturbation theory. Last updated 10 April 2014. Contents. Motivation 2. 1.1 Connection to experiments . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2. 1.2 Divergences in the standard perturbation theory . . . . . . . . . . . . . . . . 3.
We review fundamental aspects of the non-equilibrium Green function method in the simulation of nanometer electronic devices. The method is implemented into our recently developed computer package OPEDEVS to investigate transport properties of electrons in nano-scale devices and low-dimensional materials.
In this thesis we employ the non-equilibrium Green’s function (NEGF) method to study both finite and infinite systems. We develop a codebase capable of computing the steady state interacting NEGF in open systems, i.e. tight-binding leads contacting a central region, in both Hartree-Fock
This bachelor thesis is about investigating the properties of impurities in superconductors. By introducing tools like the Green’s function method and with that the spectral function, it takes a look inside the superconductor, to see what happens to the density of states when a ected by said impurity. Further, it looks into which speci c
The Green function methods for quantum many-body systems were mainly developed in the 1950’s and early 60’s. Before plunging into the formalism we briefly summarize some main
This thesis is structured as follows. In Chapter (2) we provide an extended background on the one-body Green’s function: what is its mathematical formulation, the physical significance and which quantity it can give access to. We will then detail different approaches employed nowadays for Green’s function calculations:
We develop the notion of Green functions in the presence of non-locality and derive explicit expressions for static Green functions that will be used throughout the remainder of this thesis.
We provide a systematic approach to compute different kinds of non-equilibrium Green's functions for open quantum systems which are essentially two-point correlation functions in time.
This thesis presents a novel Interpolated Factored Green Function (IFGF) method for the accelerated evaluation of the integral operators in scattering theory and other areas.
The purpose of this chapter is to present a specific numerical application of Green’s functions in tight-binding structures. The numerical technique is conventionally called the recursive Green’s function method.