hypothesis cannot be rejected

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating ​ the dependent variable or due to random chance. 

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

When do we reject the null hypothesis .

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected. 

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables. 

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a  p  -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. 

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null. 

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists. 

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter. 

Purpose of a Null Hypothesis 

• The primary purpose of the null hypothesis is to disprove an assumption. 
• Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
• A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true. 

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables. 

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study. 

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”).  However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing.  Political research quarterly ,  52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method.  American Psychologist ,  56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing.  Behavior research methods ,  43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy.  Psychological methods ,  5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test.  Psychological bulletin ,  57 (5), 416.

When Do You Reject the Null Hypothesis? (3 Examples)

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

We always use the following steps to perform a hypothesis test:

Step 1: State the null and alternative hypotheses.

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H A , is the hypothesis that the sample data is influenced by some non-random cause.

2. Determine a significance level to use.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Calculate the test statistic and p-value.

Use the sample data to calculate a test statistic and a corresponding p-value .

4. Reject or fail to reject the null hypothesis.

If the p-value is less than the significance level, then you reject the null hypothesis.

If the p-value is not less than the significance level, then you fail to reject the null hypothesis.

You can use the following clever line to remember this rule:

“If the p is low, the null must go.”

In other words, if the p-value is low enough then we must reject the null hypothesis.

The following examples show when to reject (or fail to reject) the null hypothesis for the most common types of hypothesis tests.

Example 1: One Sample t-test

A  one sample t-test  is used to test whether or not the mean of a population is equal to some value.

For example, suppose we want to know whether or not the mean weight of a certain species of turtle is equal to 310 pounds.

We go out and collect a simple random sample of 40 turtles with the following information:

• Sample size n = 40
• Sample mean weight  x  = 300
• Sample standard deviation s = 18.5

We can use the following steps to perform a one sample t-test:

Step 1: State the Null and Alternative Hypotheses

We will perform the one sample t-test with the following hypotheses:

• H 0 :  μ = 310 (population mean is equal to 310 pounds)
• H A :  μ ≠ 310 (population mean is not equal to 310 pounds)

We will choose to use a significance level of 0.05 .

We can plug in the numbers for the sample size, sample mean, and sample standard deviation into this One Sample t-test Calculator to calculate the test statistic and p-value:

• t test statistic: -3.4187
• two-tailed p-value: 0.0015

Since the p-value (0.0015) is less than the significance level (0.05) we reject the null hypothesis .

We conclude that there is sufficient evidence to say that the mean weight of turtles in this population is not equal to 310 pounds.

Example 2: Two Sample t-test

A  two sample t-test is used to test whether or not two population means are equal.

For example, suppose we want to know whether or not the mean weight between two different species of turtles is equal.

We go out and collect a simple random sample from each population with the following information:

• Sample size n 1 = 40
• Sample mean weight  x 1  = 300
• Sample standard deviation s 1 = 18.5
• Sample size n 2 = 38
• Sample mean weight  x 2  = 305
• Sample standard deviation s 2 = 16.7

We can use the following steps to perform a two sample t-test:

We will perform the two sample t-test with the following hypotheses:

• H 0 :  μ 1  = μ 2 (the two population means are equal)
• H 1 :  μ 1  ≠ μ 2 (the two population means are not equal)

We will choose to use a significance level of 0.10 .

We can plug in the numbers for the sample sizes, sample means, and sample standard deviations into this Two Sample t-test Calculator to calculate the test statistic and p-value:

• t test statistic: -1.2508
• two-tailed p-value: 0.2149

Since the p-value (0.2149) is not less than the significance level (0.10) we fail to reject the null hypothesis .

We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.

Example 3: Paired Samples t-test

A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.

For example, suppose we want to know whether or not a certain training program is able to increase the max vertical jump of college basketball players.

To test this, we may recruit a simple random sample of 20 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month:

We can use the following steps to perform a paired samples t-test:

We will perform the paired samples t-test with the following hypotheses:

• H 0 :  μ before = μ after (the two population means are equal)
• H 1 :  μ before ≠ μ after (the two population means are not equal)

We will choose to use a significance level of 0.01 .

We can plug in the raw data for each sample into this Paired Samples t-test Calculator to calculate the test statistic and p-value:

• t test statistic: -3.226
• two-tailed p-value: 0.0045

Since the p-value (0.0045) is less than the significance level (0.01) we reject the null hypothesis .

We have sufficient evidence to say that the mean vertical jump before and after participating in the training program is not equal.

Bonus: Decision Rule Calculator 

You can use this decision rule calculator to automatically determine whether you should reject or fail to reject a null hypothesis for a hypothesis test based on the value of the test statistic.

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Science, Tech, Math ›
• Statistics ›
• Inferential Statistics ›

What 'Fail to Reject' Means in a Hypothesis Test

Casarsa Guru/Getty Images

• Inferential Statistics
• Statistics Tutorials
• Probability & Games
• Descriptive Statistics
• Applications Of Statistics
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade
• Ph.D., Mathematics, Purdue University
• M.S., Mathematics, Purdue University
• B.A., Mathematics, Physics, and Chemistry, Anderson University

In statistics , scientists can perform a number of different significance tests to determine if there is a relationship between two phenomena. One of the first they usually perform is a null hypothesis test. In short, the null hypothesis states that there is no meaningful relationship between two measured phenomena. After a performing a test, scientists can:

• Reject the null hypothesis (meaning there is a definite, consequential relationship between the two phenomena), or
• Fail to reject the null hypothesis (meaning the test has not identified a consequential relationship between the two phenomena)

Key Takeaways: The Null Hypothesis

• In a test of significance, the null hypothesis states that there is no meaningful relationship between two measured phenomena.

• By comparing the null hypothesis to an alternative hypothesis, scientists can either reject or fail to reject the null hypothesis.

• The null hypothesis cannot be positively proven. Rather, all that scientists can determine from a test of significance is that the evidence collected does or does not disprove the null hypothesis.

It is important to note that a failure to reject does not mean that the null hypothesis is true—only that the test did not prove it to be false. In some cases, depending on the experiment, a relationship may exist between two phenomena that is not identified by the experiment. In such cases, new experiments must be designed to rule out alternative hypotheses.

Null vs. Alternative Hypothesis

The null hypothesis is considered the default in a scientific experiment . In contrast, an alternative hypothesis is one that claims that there is a meaningful relationship between two phenomena. These two competing hypotheses can be compared by performing a statistical hypothesis test, which determines whether there is a statistically significant relationship between the data.

For example, scientists studying the water quality of a stream may wish to determine whether a certain chemical affects the acidity of the water. The null hypothesis—that the chemical has no effect on the water quality—can be tested by measuring the pH level of two water samples, one of which contains some of the chemical and one of which has been left untouched. If the sample with the added chemical is measurably more or less acidic—as determined through statistical analysis—it is a reason to reject the null hypothesis. If the sample's acidity is unchanged, it is a reason to not reject the null hypothesis.

When scientists design experiments, they attempt to find evidence for the alternative hypothesis. They do not try to prove that the null hypothesis is true. The null hypothesis is assumed to be an accurate statement until contrary evidence proves otherwise. As a result, a test of significance does not produce any evidence pertaining to the truth of the null hypothesis.

Failing to Reject vs. Accept

In an experiment, the null hypothesis and the alternative hypothesis should be carefully formulated such that one and only one of these statements is true. If the collected data supports the alternative hypothesis, then the null hypothesis can be rejected as false. However, if the data does not support the alternative hypothesis, this does not mean that the null hypothesis is true. All it means is that the null hypothesis has not been disproven—hence the term "failure to reject." A "failure to reject" a hypothesis should not be confused with acceptance.

In mathematics, negations are typically formed by simply placing the word “not” in the correct place. Using this convention, tests of significance allow scientists to either reject or not reject the null hypothesis. It sometimes takes a moment to realize that “not rejecting” is not the same as "accepting."

Null Hypothesis Example

In many ways, the philosophy behind a test of significance is similar to that of a trial. At the beginning of the proceedings, when the defendant enters a plea of “not guilty,” it is analogous to the statement of the null hypothesis. While the defendant may indeed be innocent, there is no plea of “innocent” to be formally made in court. The alternative hypothesis of “guilty” is what the prosecutor attempts to demonstrate.

The presumption at the outset of the trial is that the defendant is innocent. In theory, there is no need for the defendant to prove that he or she is innocent. The burden of proof is on the prosecuting attorney, who must marshal enough evidence to convince the jury that the defendant is guilty beyond a reasonable doubt. Likewise, in a test of significance, a scientist can only reject the null hypothesis by providing evidence for the alternative hypothesis.

If there is not enough evidence in a trial to demonstrate guilt, then the defendant is declared “not guilty.” This claim has nothing to do with innocence; it merely reflects the fact that the prosecution failed to provide enough evidence of guilt. In a similar way, a failure to reject the null hypothesis in a significance test does not mean that the null hypothesis is true. It only means that the scientist was unable to provide enough evidence for the alternative hypothesis.

For example, scientists testing the effects of a certain pesticide on crop yields might design an experiment in which some crops are left untreated and others are treated with varying amounts of pesticide. Any result in which the crop yields varied based on pesticide exposure—assuming all other variables are equal—would provide strong evidence for the alternative hypothesis (that the pesticide does affect crop yields). As a result, the scientists would have reason to reject the null hypothesis.

• Type I and Type II Errors in Statistics
• Null Hypothesis and Alternative Hypothesis
• An Example of Chi-Square Test for a Multinomial Experiment
• The Difference Between Type I and Type II Errors in Hypothesis Testing
• What Level of Alpha Determines Statistical Significance?
• What Is the Difference Between Alpha and P-Values?
• How to Find Critical Values with a Chi-Square Table
• The Runs Test for Random Sequences
• An Example of a Hypothesis Test
• What Is ANOVA?
• Example of a Permutation Test
• Degrees of Freedom for Independence of Variables in Two-Way Table
• How to Find Degrees of Freedom in Statistics
• Example of an ANOVA Calculation
• Confidence Intervals: 4 Common Mistakes
• How to Construct a Confidence Interval for a Population Proportion

How to accept or reject a hypothesis?

A hypothesis is a proposed statement to explore a possible theory. Many studies in the fields of social sciences, sciences, and mathematics make use of hypothesis testing to prove a theory. Assumptions in a hypothesis help in making predictions. It is presented in the form of null and alternate hypotheses. When a hypothesis is presented negatively (for example, TV advertisements do not affect consumer behavior), it is called a null hypothesis. This article explains the conditions to accept or reject a hypothesis.

Why is it important to reject the null hypothesis?

A null hypothesis is a statement that describes that there is no difference in the assumed characteristics of the population. For example, in a study wherein the impact of the level of education on the efficiency of the employee need to be determined, null (Ho) and alternate (HA) hypothesis would be:

In the above-stated null hypothesis, there is very little chance of a relationship between both the variables (education and employee’s efficiency). When a null hypothesis is accepted, it shows that the study has a lack of evidence in showing any significant connection between the variables. This could be due to problems with the data such as:

• high variability,
• small sample size,
• inappropriate sample and,
• wrong data testing method.

Hence, for efficient, appropriate, and reliable results, it is suggested to reject the null hypothesis.

Conditions for rejecting a null hypothesis

Rejection of the null hypothesis provides sufficient evidence for supporting the perception of the researcher. Thus, a statistician always prefers to reject the null hypothesis. However, there are certain conditions which need to be fulfilled for the required results i.e.

Condition 1: Sample data should be reasonably random

A random sample is the one every person in the sample universe has an equal possibility of being selected for the analysis. Random sampling is necessary for deriving accurate results and rejecting the null hypothesis. This is because when a sample is randomly selected, characteristic traits of each participant in the study are the same, so there is no error in decision making. For example, in the sample hypothesis, instead of collecting data from all employees, the data was collected from only the board members of the company. This hypothesis testing would not provide good results as the sample does not represent all the employees of the company.

Condition 2: Distribution of the sample should be known

A dataset can be of two types: normally distributed or skewed. Normally distributed datasets require application of parametric tests i.e. Z-test, T-test, χ2-test, and F-distribution. On the other hand, skewed dataset uses non-parametric test i.e. Wilcoxon rank sum test, Wilcoxon signed rank test, and Kruskal Wallis test. For reliable hypothesis test result, it is essential that the distribution of the sample be tested.

Condition 3: Value of test statistic should not fall in the rejection region

Test statistic value is compared with critical value when the null hypothesis is true (critical value). If the test statistic is more extreme as compared to the critical value, then the null hypothesis would be rejected.

For example, in the sample hypothesis if the sample size is 50 and the significance level of the study is 5% then the critical value for the given two-tailed test would be 1.960. Hence, null hypothesis would be rejected if,

Condition 4: P-value should be less than the significance of the study

P-value represents the probability that the null hypothesis true. In order to reject the null hypothesis, it is essential that the p-value should be less that the significance or the precision level considered for the study. Hence,

• Reject null hypothesis (H0) if ‘p’ value  < statistical significance (0.01/0.05/0.10)
• Accept null hypothesis (H0) if ‘p’ value > statistical significance (0.01/0.05/0.10)

For example, in the sample hypothesis if the considered statistical significance level is 5% and the p-value of the model is 0.12. Hence, the hypothesis of having no significant impact would not be rejected as 0.12 > 0.05.

Important points to note

While making the final decision of the hypothesis, these points should be noted i.e.

• A large sample size i.e. at least greater than 30 should be considered. As per the Central Limit Theorem (CLT) large sample size i.e. at least greater than 30 is considered to be approximately normally distributed.
• For deriving the results either p-value approach or rejection approach could be used. However, the p-value is a more preferable approach.
• Statistical significance should be maintained at a minimum level.
• The choice of the rejection region should be appropriately made by verifying the direction of the alternative hypothesis.
• Priya Chetty

I am a management graduate with specialisation in Marketing and Finance. I have over 12 years' experience in research and analysis. This includes fundamental and applied research in the domains of management and social sciences. I am well versed with academic research principles. Over the years i have developed a mastery in different types of data analysis on different applications like SPSS, Amos, and NVIVO. My expertise lies in inferring the findings and creating actionable strategies based on them. 

Over the past decade I have also built a profile as a researcher on Project Guru's Knowledge Tank division. I have penned over 200 articles that have earned me 400+ citations so far. My Google Scholar profile can be accessed here . 

I now consult university faculty through Faculty Development Programs (FDPs) on the latest developments in the field of research. I also guide individual researchers on how they can commercialise their inventions or research findings. Other developments im actively involved in at Project Guru include strengthening the "Publish" division as a bridge between industry and academia by bringing together experienced research persons, learners, and practitioners to collaboratively work on a common goal. 

I am a Senior Analyst at Project Guru, a research and analytics firm based in Gurugram since 2012. I hold a master’s degree in economics from Amity University (2019). Over 4 years, I have worked on worked on various research projects using a range of research tools like SPSS, STATA, VOSViewer, Python, EVIEWS, and NVIVO. My core strength lies in data analysis related to Economics, Accounting, and Financial Management fields.

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on WhatsApp (Opens in new window)
• Click to share on Telegram (Opens in new window)

Notify me of follow-up comments by email.

proofreading

• High School
• You don't have any recent items yet.
• You don't have any courses yet.
• You don't have any books yet.
• You don't have any Studylists yet.
• Herzing University

Which hypotheses can be rejected alternate only null only both

Subject : Other

Relevant documents

Documents that match the answer

Answer Created with AI

Hypothesis testing.

In hypothesis testing, we start with two hypotheses:

Null Hypothesis (H0) : This is a statement of no effect or no difference. It's the hypothesis that we aim to challenge and possibly reject.

Alternative Hypothesis (H1 or Ha) : This is a statement that indicates the presence of an effect or a difference. It's what we consider as an alternative to the null hypothesis.

Rejection of Hypotheses

Null Hypothesis (H0) : The null hypothesis can be rejected if the test statistic falls in the critical region, i.e., if the p-value is less than the significance level (usually 0.05). This means that the observed data is highly unlikely under the null hypothesis, leading us to reject it.

Alternative Hypothesis (H1 or Ha) : The alternative hypothesis cannot be "rejected". Instead, we either reject the null hypothesis in favor of the alternative, or we fail to reject the null hypothesis, which does not necessarily prove it true.

So, to answer your question:

• The null hypothesis can be rejected.
• The alternative hypothesis cannot be rejected, but can be accepted if the null hypothesis is rejected.
• It's not possible to reject both the null and alternative hypotheses . If we reject the null hypothesis, we are essentially accepting the alternative hypothesis. If we fail to reject the null hypothesis, we are not making any statement about the alternative hypothesis.

Here's a simple table to illustrate this:

• Discover more from: Statistics MA 320 Herzing University 85   Documents Go to course

Related Answered Questions

• Statistics (MA 320) 5 days ago Were the relationships they discovered in their research strong enough to use to predict one variable from the other in the post, What is the real-world significance of the findings they described in the post "The two variables I chose to focus on in this discussion are blood pressure and heart rate. These variables are essential in the nursing field as they provide valuable insights into a patient’s health. By using these factors, nurses can assess a patient’s condition and develop better care plans. From my research, I have concluded that there is a correlation between blood pressure and heart rate. Blood pressure is the force with which blood flows against the walls of the arteries. Normal blood pressure is less than 120/80 mmHg (What It Means If You Have Low Blood Pressure but a High Heart Rate, n.d.). If the numbers fall significantly below this range, it is considered hypotension, while higher numbers indicate hypertension. Heart rate, on the other hand, refers to the number of times the heart beats per minute. The normal resting range is 60 to 100 beats per minute (What It Means If You Have Low Blood Pressure but a High Heart Rate, n.d.). Both of these variables can be influenced by various factors. A study found a correlation between higher resting heart rates and elevated blood pressure in adolescents. It showed that with each increased heartbeat, there was a 0.090 mmHg increase in blood pressure in both males and females (Christofaro et al., 2017). This study shows the relationship between heart rate and blood pressure, demonstrating that a change in one can lead to a change in the other" (more) 0 1 Answers
• Statistics (MA 320) 5 days ago State whether you agree with the meaning of the relationship as described in the post? Can you think of other variables that might help explain the relationship between the two-variable chosen in the post? If no relationship was found, can you offer any reasons why not? " The two variables I chose to focus on in this discussion are blood pressure and heart rate. These variables are essential in the nursing field as they provide valuable insights into a patient’s health. By using these factors, nurses can assess a patient’s condition and develop better care plans. From my research, I have concluded that there is a correlation between blood pressure and heart rate. Blood pressure is the force with which blood flows against the walls of the arteries. Normal blood pressure is less than 120/80 mmHg (What It Means If You Have Low Blood Pressure but a High Heart Rate, n.d.). If the numbers fall significantly below this range, it is considered hypotension, while higher numbers indicate hypertension. Heart rate, on the other hand, refers to the number of times the heart beats per minute. The normal resting range is 60 to 100 beats per minute (What It Means If You Have Low Blood Pressure but a High Heart Rate, n.d.). Both of these variables can be influenced by various factors. A study found a correlation between higher resting heart rates and elevated blood pressure in adolescents. It showed that with each increased heartbeat, there was a 0.090 mmHg increase in blood pressure in both males and females (Christofaro et al., 2017). This study shows the relationship between heart rate and blood pressure, demonstrating that a change in one can lead to a change in the other." (more) 0 1 Answers
• Statistics (MA 320) 5 days ago What is the real-world significance of the findings they described in the post"Hypertension is a fairly common clinical finding in many patients today. It can be affected by a variety of things such as diet, activity, lifestyle, medications, and other disease processes. Higher blood pressures can have effects on the circulatory system, respiratory system, and many other bodily functions. One other clinical finding that can be affected by hypertension is a person’s heart rate. In the HARVEST study, 15% of patients with hypertension had resting heart rates over 85bpm and 27% had resting heart rates over 80bpm (Reule & Drawz, 2012). According to the AHA, a higher resting heart rate is associated to a higher risk of developing sustained hypertension and in studies that have been performed, there is evidence of positive regression between heart rate and hypertension (Julius et al., 1997). In a study performed by the World Health Organization-Cardiovascular Disease and Alimentary Comparison, they showed a positive regression and positive correlation between increased heart rate and increased blood pressure (Liu L, Mizushima S, Ikeda K, Nara Y, Yamori Y, 2010). Their results showed that an increase of one beat per minute correlated to a systolic blood pressure increase of 0.27mmHg and a diastolic blood pressure increase of 0.09mmHg (Liu L, Mizushima S, Ikeda K, Nara Y, Yamori Y, 2010). This shows that a higher resting heart rate directly correlates to an increased blood pressure" (more) 0 1 Answers
• Statistics (MA 320) 5 days ago If no relationship was found, in the post, can you offer any reasons why not, Were the relationships they discovered in their research strong enough to use to predict one variable from the other."Hypertension is a fairly common clinical finding in many patients today. It can be affected by a variety of things such as diet, activity, lifestyle, medications, and other disease processes. Higher blood pressures can have effects on the circulatory system, respiratory system, and many other bodily functions. One other clinical finding that can be affected by hypertension is a person’s heart rate. In the HARVEST study, 15% of patients with hypertension had resting heart rates over 85bpm and 27% had resting heart rates over 80bpm (Reule & Drawz, 2012). According to the AHA, a higher resting heart rate is associated to a higher risk of developing sustained hypertension and in studies that have been performed, there is evidence of positive regression between heart rate and hypertension (Julius et al., 1997). In a study performed by the World Health Organization-Cardiovascular Disease and Alimentary Comparison, they showed a positive regression and positive correlation between increased heart rate and increased blood pressure (Liu L, Mizushima S, Ikeda K, Nara Y, Yamori Y, 2010). Their results showed that an increase of one beat per minute correlated to a systolic blood pressure increase of 0.27mmHg and a diastolic blood pressure increase of 0.09mmHg (Liu L, Mizushima S, Ikeda K, Nara Y, Yamori Y, 2010). This shows that a higher resting heart rate directly correlates to an increased blood pressure" (more) 0 1 Answers
• Statistics (MA 320) 5 days ago State whether you agree with the meaning of the relationship as described by the post and Can you think of other variables that might help explain the relationship between the two variables they chose of the this post"Hypertension is a fairly common clinical finding in many patients today. It can be affected by a variety of things such as diet, activity, lifestyle, medications, and other disease processes. Higher blood pressures can have effects on the circulatory system, respiratory system, and many other bodily functions. One other clinical finding that can be affected by hypertension is a person’s heart rate. In the HARVEST study, 15% of patients with hypertension had resting heart rates over 85bpm and 27% had resting heart rates over 80bpm (Reule & Drawz, 2012). According to the AHA, a higher resting heart rate is associated to a higher risk of developing sustained hypertension and in studies that have been performed, there is evidence of positive regression between heart rate and hypertension (Julius et al., 1997). In a study performed by the World Health Organization-Cardiovascular Disease and Alimentary Comparison, they showed a positive regression and positive correlation between increased heart rate and increased blood pressure (Liu L, Mizushima S, Ikeda K, Nara Y, Yamori Y, 2010). Their results showed that an increase of one beat per minute correlated to a systolic blood pressure increase of 0.27mmHg and a diastolic blood pressure increase of 0.09mmHg (Liu L, Mizushima S, Ikeda K, Nara Y, Yamori Y, 2010). This shows that a higher resting heart rate directly correlates to an increased blood pressure". (more) 0 1 Answers
• Statistics (MA 320) 6 days ago TRUE/FALSE: Although the math model used in Simple Linear Regression is linear, the estimated model can be any shape. False True (more) 0 1 Answers

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.1 hypothesis testing (critical value approach).

The critical value approach involves determining "likely" or "unlikely" by determining whether or not the observed test statistic is more extreme than would be expected if the null hypothesis were true. That is, it entails comparing the observed test statistic to some cutoff value, called the " critical value ." If the test statistic is more extreme than the critical value, then the null hypothesis is rejected in favor of the alternative hypothesis. If the test statistic is not as extreme as the critical value, then the null hypothesis is not rejected.

Specifically, the four steps involved in using the critical value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. To conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Determine the critical value by finding the value of the known distribution of the test statistic such that the probability of making a Type I error — which is denoted \(\alpha\) (greek letter "alpha") and is called the " significance level of the test " — is small (typically 0.01, 0.05, or 0.10).
• Compare the test statistic to the critical value. If the test statistic is more extreme in the direction of the alternative than the critical value, reject the null hypothesis in favor of the alternative hypothesis. If the test statistic is less extreme than the critical value, do not reject the null hypothesis.

Example S.3.1.1

Mean gpa section  .

In our example concerning the mean grade point average, suppose we take a random sample of n = 15 students majoring in mathematics. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right-Tailed

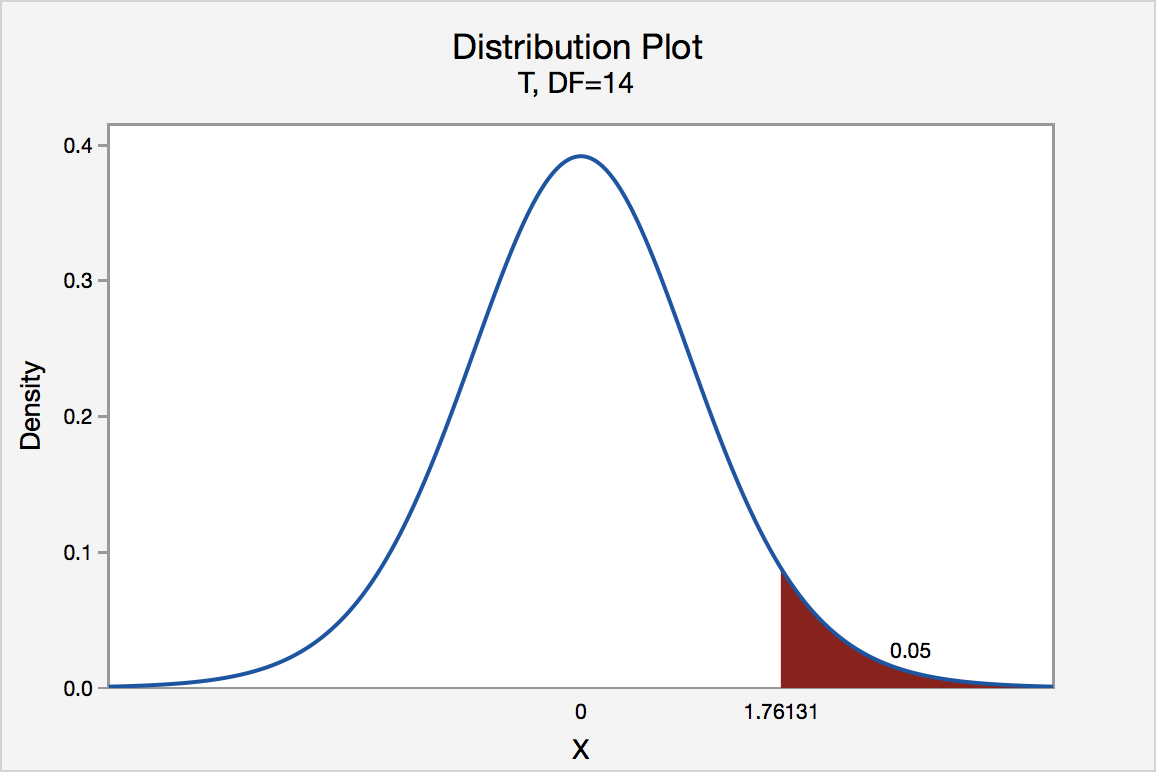
The critical value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the t -value, denoted t \(\alpha\) , n - 1 , such that the probability to the right of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value t 0.05,14 is 1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3 if the test statistic t * is greater than 1.7613. Visually, the rejection region is shaded red in the graph.

Left-Tailed

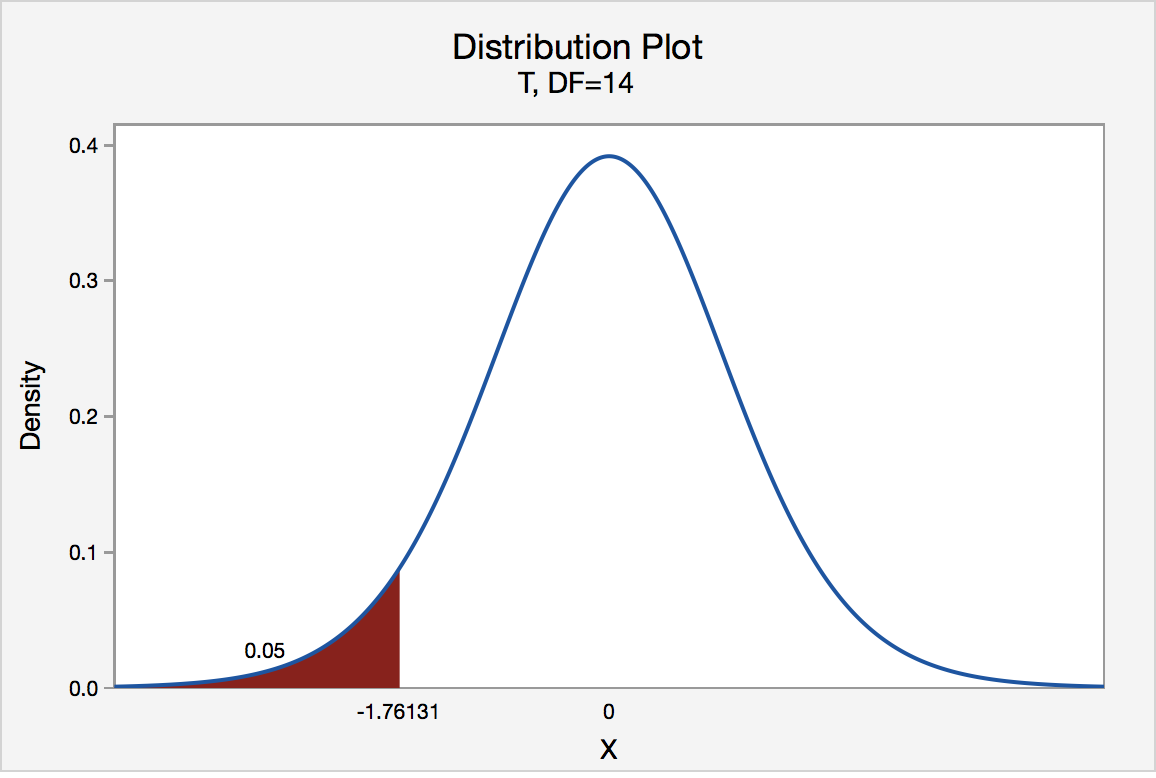
The critical value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the t -value, denoted -t ( \(\alpha\) , n - 1) , such that the probability to the left of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value -t 0.05,14 is -1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3 if the test statistic t * is less than -1.7613. Visually, the rejection region is shaded red in the graph.

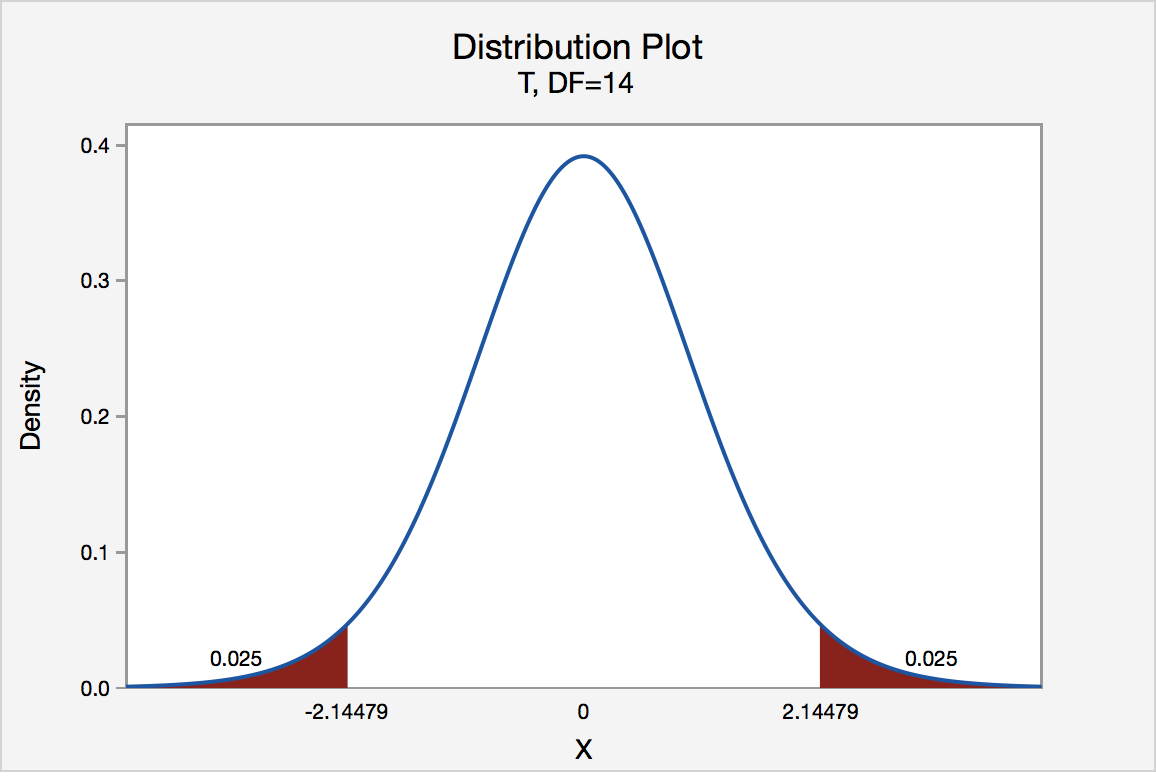
There are two critical values for the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 — one for the left-tail denoted -t ( \(\alpha\) / 2, n - 1) and one for the right-tail denoted t ( \(\alpha\) / 2, n - 1) . The value - t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the left of it is \(\alpha\)/2, and the value t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the right of it is \(\alpha\)/2. It can be shown using either statistical software or a t -table that the critical value -t 0.025,14 is -2.1448 and the critical value t 0.025,14 is 2.1448. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3 if the test statistic t * is less than -2.1448 or greater than 2.1448. Visually, the rejection region is shaded red in the graph.